3.4. scikit-learn:Python中的机器学习¶
作者:Gael Varoquaux

3.4.1. 引言:问题设置¶
3.4.1.1. 什么是机器学习?¶
提示
机器学习是关于构建具有可调参数的程序,这些参数会自动调整,以便通过适应先前看到的数据来改善其行为。
机器学习可以被认为是人工智能的一个子领域,因为这些算法可以被视为构建模块,使计算机能够通过某种方式泛化来学习更智能地行为,而不是像数据库系统那样仅仅存储和检索数据项。
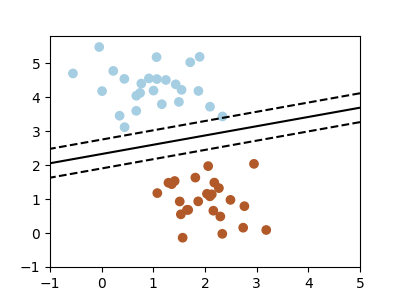
分类问题¶
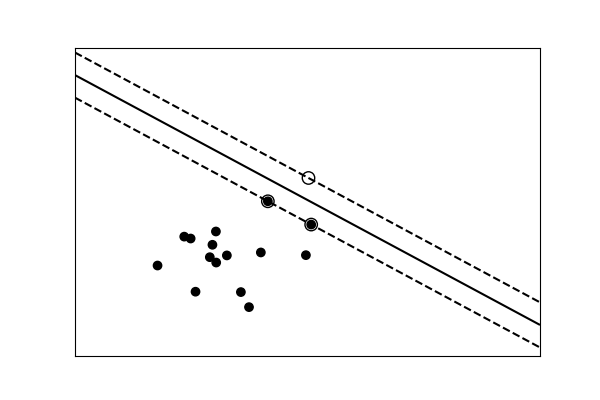
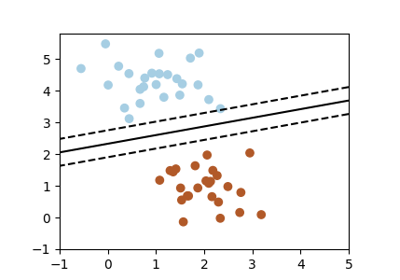
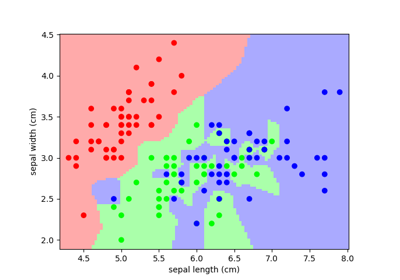
我们将在本文中研究两个非常简单的机器学习任务。第一个是分类任务:该图显示了二维数据的集合,根据两个不同的类别标签进行着色。可以使用分类算法在两个数据点簇之间绘制分界线。
通过绘制这条分隔线,我们学习了一个可以泛化到新数据的模型:如果你要将另一个未标记的点放到平面上,此算法现在可以预测它是蓝色点还是红色点。
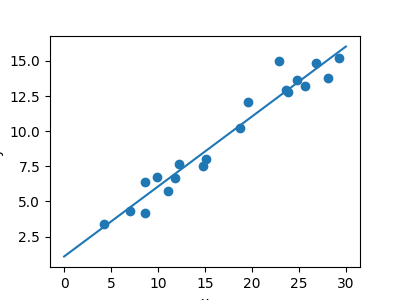
回归问题¶
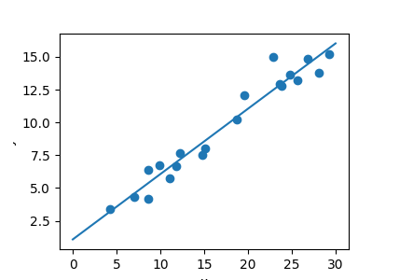
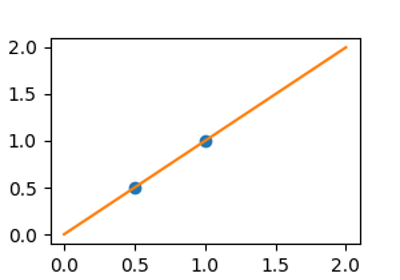
我们将要研究的下一个简单任务是回归任务:一组数据的一个简单的最佳拟合线。
同样,这是将模型拟合到数据的示例,但我们这里关注的是模型可以对新数据进行泛化。模型是从训练数据中学习到的,可用于预测测试数据的结果:在这里,我们可能会得到一个x值,模型将允许我们预测y值。
3.4.1.2. scikit-learn中的数据¶
数据矩阵¶
scikit-learn中实现的机器学习算法期望数据存储在二维数组或矩阵中。数组可以是numpy数组,或者在某些情况下是scipy.sparse矩阵。数组的大小应为[n_samples, n_features]
n_samples:样本数:每个样本都是要处理(例如分类)的项目。样本可以是文档、图片、声音、视频、天文对象、数据库或CSV文件中的行,或者任何可以用一组固定的定量特征来描述的内容。
n_features:特征数或可用于以定量方式描述每个项目的不同特征。特征通常是实数值,但在某些情况下可能是布尔值或离散值。
提示
特征的数量必须预先确定。但是,它可以具有非常高的维度(例如,数百万个特征),其中大多数对于给定样本而言为零。在这种情况下,scipy.sparse矩阵很有用,因为它们比NumPy数组更节省内存。
一个简单的示例:鸢尾花数据集¶
应用问题¶
作为简单数据集的示例,让我们看一下scikit-learn存储的鸢尾花数据。假设我们想识别鸢尾花的种类。数据包括三种不同鸢尾花的测量结果。
|
|
|
|---|---|---|
山鸢尾 |
杂色鸢尾 |
维吉尼亚鸢尾 |
请记住,每个样本的特征数量必须是固定的,并且特征编号i对于每个样本必须是相同类型的量。
使用Scikit-learn加载鸢尾花数据¶
Scikit-learn有一组非常简单的关于这些鸢尾花种类的数据。数据包括以下内容:
鸢尾花数据集中的特征
萼片长度(厘米)
萼片宽度(厘米)
花瓣长度(厘米)
花瓣宽度(厘米)
要预测的目标类别
山鸢尾
杂色鸢尾
维吉尼亚鸢尾
scikit-learn将鸢尾花CSV文件的副本以及将其加载到NumPy数组中的函数嵌入其中。
>>> from sklearn.datasets import load_iris
>>> iris = load_iris()
注意
导入sklearn 请注意,scikit-learn导入为sklearn
每个样本花的特征存储在数据集的data属性中。
>>> print(iris.data.shape)
(150, 4)
>>> n_samples, n_features = iris.data.shape
>>> print(n_samples)
150
>>> print(n_features)
4
>>> print(iris.data[0])
[5.1 3.5 1.4 0.2]
有关每个样本类别的信息存储在数据集的target属性中。
>>> print(iris.target.shape)
(150,)
>>> print(iris.target)
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2]
类别的名称存储在最后一个属性中,即target_names。
>>> print(iris.target_names)
['setosa' 'versicolor' 'virginica']
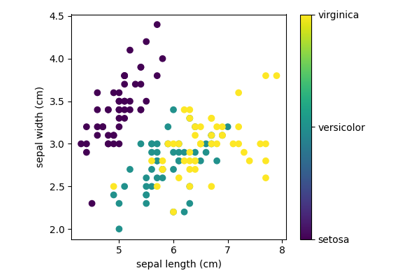
此数据是四维的,但我们可以使用散点图一次可视化两个维度。
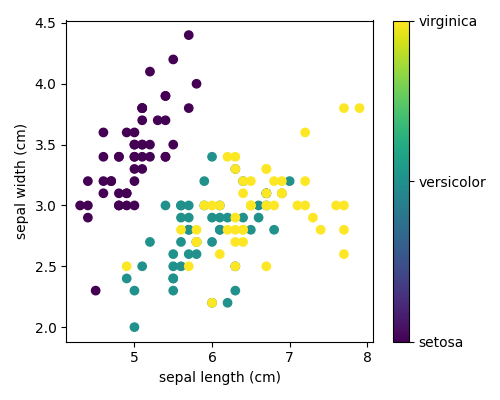
3.4.2. 使用scikit-learn进行机器学习的基本原理¶
3.4.2.1. 介绍scikit-learn估计器对象¶
scikit-learn中每个算法都通过“估计器”对象公开。例如,线性回归是:sklearn.linear_model.LinearRegression
>>> from sklearn.linear_model import LinearRegression
估计器参数:可以在实例化估计器时设置所有估计器参数。
>>> model = LinearRegression(n_jobs=1)
>>> print(model)
LinearRegression(n_jobs=1)
拟合数据¶
让我们使用numpy创建一些简单的数据。
>>> import numpy as np
>>> x = np.array([0, 1, 2])
>>> y = np.array([0, 1, 2])
>>> X = x[:, np.newaxis] # The input data for sklearn is 2D: (samples == 3 x features == 1)
>>> X
array([[0],
[1],
[2]])
>>> model.fit(X, y)
LinearRegression(n_jobs=1)
估计的参数:当数据使用估计器拟合时,会根据手头的数据估计参数。所有估计的参数都是估计器对象的属性,以下划线结尾。
>>> model.coef_
array([1.])
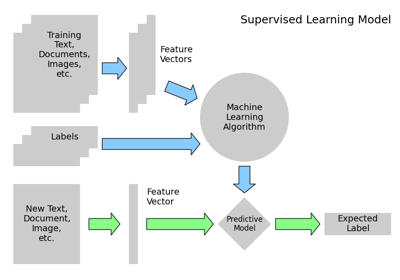
3.4.2.2. 监督学习:分类和回归¶
在监督学习中,我们有一个包含特征和标签的数据集。任务是构建一个能够根据特征集预测对象标签的估计器。一个相对简单的示例是根据一组花卉测量结果预测鸢尾花的种类。这是一个相对简单的任务。一些更复杂的示例包括:
给定通过望远镜获得的对象的多色图像,确定该对象是恒星、类星体还是星系。
给定一个人的照片,识别照片中的人。
给定一个人观看过的电影列表及其对电影的个人评分,推荐他们可能喜欢的电影列表(所谓的推荐系统:一个著名的示例是Netflix奖)。
提示
这些任务的共同点是,与需要确定的对象相关联的一个或多个未知量需要根据其他观察到的量来确定。
监督学习进一步细分为两个类别:**分类**和**回归**。在分类中,标签是离散的,而在回归中,标签是连续的。例如,在天文领域,确定一个物体是恒星、星系还是类星体的任务就是一个分类问题:标签来自三个不同的类别。另一方面,我们可能希望根据这些观测结果来估计物体的年龄:这将是一个回归问题,因为标签(年龄)是一个连续的量。
**分类**:K近邻 (kNN) 是最简单的学习策略之一:给定一个新的、未知的观测值,在你的参考数据库中查找特征最接近的那些,并分配主要类别。让我们在我们的鸢尾花分类问题上试一试。
from sklearn import neighbors, datasets
iris = datasets.load_iris()
X, y = iris.data, iris.target
knn = neighbors.KNeighborsClassifier(n_neighbors=1)
knn.fit(X, y)
# What kind of iris has 3cm x 5cm sepal and 4cm x 2cm petal?
print(iris.target_names[knn.predict([[3, 5, 4, 2]])])
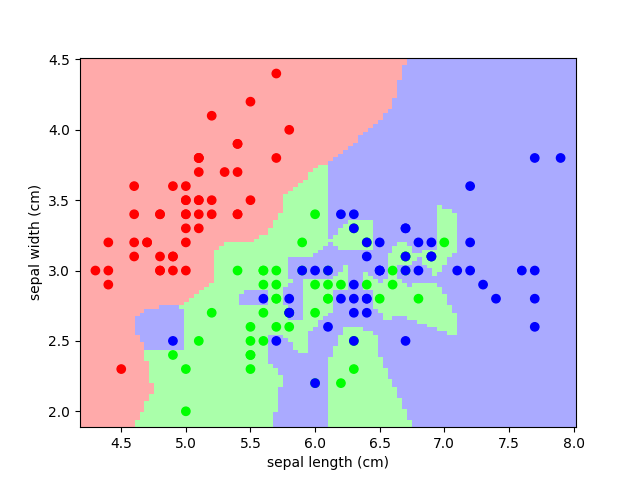
萼片空间的图和KNN的预测¶
**回归**:最简单的回归设置是线性回归。
from sklearn.linear_model import LinearRegression
# x from 0 to 30
rng = np.random.default_rng()
x = 30 * rng.random((20, 1))
# y = a*x + b with noise
y = 0.5 * x + 1.0 + rng.normal(size=x.shape)
# create a linear regression model
model = LinearRegression()
model.fit(x, y)
# predict y from the data
x_new = np.linspace(0, 30, 100)
y_new = model.predict(x_new[:, np.newaxis])

简单的线性回归图。¶
3.4.2.3. Scikit-learn 的估计器接口回顾¶
Scikit-learn 努力在所有方法中保持统一的接口,我们将在下面看到这些示例。给定一个名为 model 的 scikit-learn 估计器对象,以下方法可用
- 在**所有估计器**中:
model.fit():拟合训练数据。对于监督学习应用,它接受两个参数:数据X和标签y(例如model.fit(X, y))。对于无监督学习应用,它只接受一个参数,即数据X(例如model.fit(X))。
- 在**监督估计器**中:
model.predict():给定一个训练好的模型,预测新数据集的标签。此方法接受一个参数,即新数据X_new(例如model.predict(X_new)),并返回数组中每个对象的学习标签。model.predict_proba():对于分类问题,一些估计器也提供此方法,它返回新观测值具有每个类别标签的概率。在这种情况下,model.predict()返回概率最高的标签。model.score():对于分类或回归问题,大多数(所有?)估计器都实现了评分方法。分数在 0 到 1 之间,分数越大表示拟合越好。
- 在**无监督估计器**中:
model.transform():给定一个无监督模型,将新数据转换为新的基础。这也接受一个参数X_new,并根据无监督模型返回数据的新的表示。model.fit_transform():一些估计器实现了此方法,它更有效地对相同输入数据执行拟合和转换。
3.4.2.4. 正则化:它是什么以及为什么需要它¶
偏好更简单的模型¶
**训练误差**假设你正在使用一个 1-近邻估计器。你期望在你的训练集上出现多少错误?
训练集误差不是衡量预测性能的良好指标。你需要留出一个测试集。
一般来说,我们应该接受训练集上的错误。
**正则化的一个例子**正则化的核心思想是,我们将偏好更简单的模型,对于“更简单”的某种定义,即使它们在训练集上导致更多错误。
例如,让我们使用 9 阶多项式生成带噪声的数据。
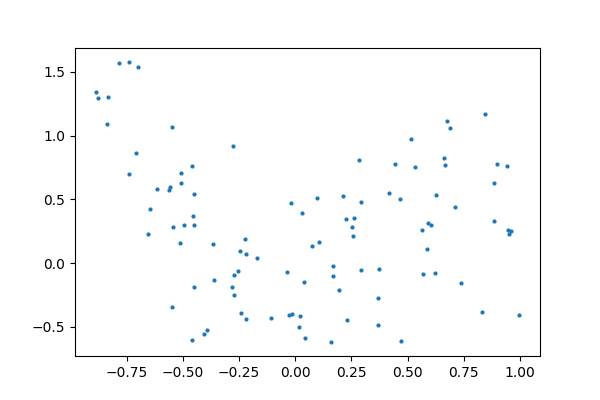
现在,让我们将 4 阶和 9 阶多项式拟合到数据中。
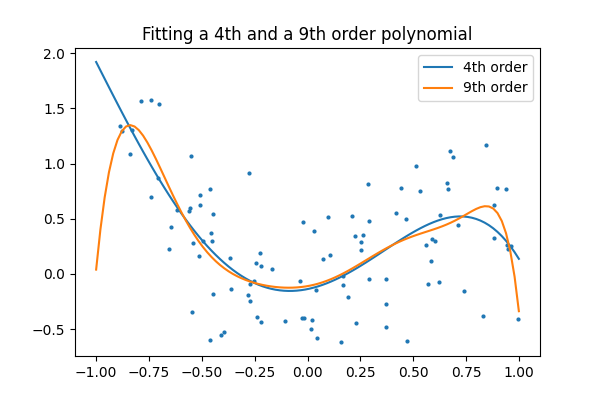
凭肉眼,你更喜欢哪个模型,4 阶模型还是 9 阶模型?
让我们看看真实情况。
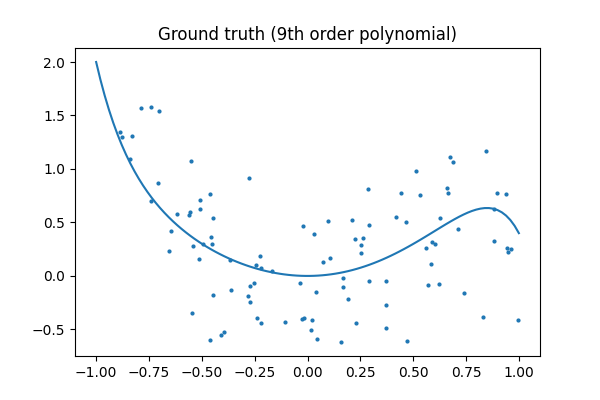
提示
正则化在机器学习中无处不在。大多数 scikit-learn 估计器都有一个参数来调整正则化的数量。例如,对于 k-NN,它是“k”,用于做出决策的最近邻的数量。k=1 等于没有正则化:训练集上的误差为 0,而较大的 k 将推动特征空间中更平滑的决策边界。
用于分类的简单模型与复杂模型¶
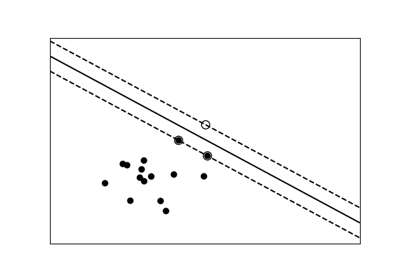
线性分离 |
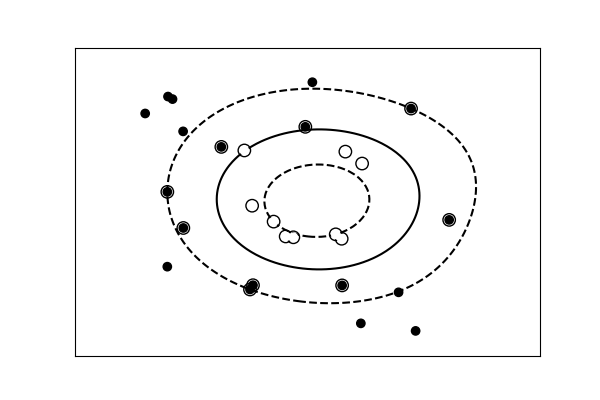
非线性分离 |
提示
对于分类模型,将类别分开的决策边界表达了模型的复杂性。例如,基于特征的线性组合做出决策的线性模型,比非线性模型更复杂。
3.4.3. 监督学习:手写数字的分类¶
3.4.3.1. 数据的性质¶
在本节中,我们将应用 scikit-learn 来进行手写数字的分类。这将比我们之前看到的鸢尾花分类更进一步:我们将讨论一些可用于评估分类模型有效性的指标。
>>> from sklearn.datasets import load_digits
>>> digits = load_digits()

让我们可视化数据并提醒我们正在查看什么(点击图片查看完整代码)
# plot the digits: each image is 8x8 pixels
for i in range(64):
ax = fig.add_subplot(8, 8, i + 1, xticks=[], yticks=[])
ax.imshow(digits.images[i], cmap=plt.cm.binary, interpolation='nearest')
3.4.3.2. 在其主成分上可视化数据¶
对于许多问题,一个好的第一步是使用降维技术来可视化数据。我们将从最直接的一个开始,主成分分析 (PCA)。
PCA 寻找特征的正交线性组合,这些组合显示出最大的方差,因此,可以帮助你很好地了解数据集的结构。
>>> from sklearn.decomposition import PCA
>>> pca = PCA(n_components=2)
>>> proj = pca.fit_transform(digits.data)
>>> plt.scatter(proj[:, 0], proj[:, 1], c=digits.target)
<matplotlib.collections.PathCollection object at ...>
>>> plt.colorbar()
<matplotlib.colorbar.Colorbar object at ...>
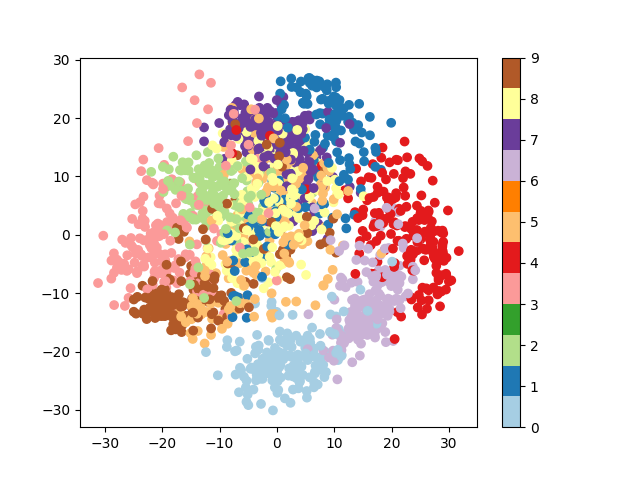
3.4.3.3. 高斯朴素贝叶斯分类¶
对于大多数分类问题,最好有一个简单、快速的方法来提供一个快速的基线分类。如果简单快速的方法足够了,那么我们就不必浪费 CPU 周期在更复杂的模型上。如果不是,我们可以使用简单方法的结果来为我们提供有关数据的线索。
一个值得记住的好方法是高斯朴素贝叶斯 (sklearn.naive_bayes.GaussianNB)。
提示
高斯朴素贝叶斯独立地对每个特征上的每个训练标签拟合一个高斯分布,并使用它来快速给出粗略的分类。它通常对于现实世界的数据来说不够准确,但可以表现出惊人的良好性能,例如在文本数据上。
>>> from sklearn.naive_bayes import GaussianNB
>>> from sklearn.model_selection import train_test_split
>>> # split the data into training and validation sets
>>> X_train, X_test, y_train, y_test = train_test_split(
... digits.data, digits.target, random_state=42)
>>> # train the model
>>> clf = GaussianNB()
>>> clf.fit(X_train, y_train)
GaussianNB()
>>> # use the model to predict the labels of the test data
>>> predicted = clf.predict(X_test)
>>> expected = y_test
>>> print(predicted)
[6 9 3 7 2 2 5 8 5 2 1 1 7 0 4 8 3 7 8 8 4 3 9 7 5 6 3 5 6 3...]
>>> print(expected)
[6 9 3 7 2 1 5 2 5 2 1 9 4 0 4 2 3 7 8 8 4 3 9 7 5 6 3 5 6 3...]
如上所述,我们将数字与预测标签一起绘制,以了解分类的效果如何。

3.4.3.4. 性能的定量测量¶
我们希望在不诉诸绘制示例的情况下测量估计器的性能。一个简单的方法可能是简单地比较匹配的数量。
>>> matches = (predicted == expected)
>>> print(matches.sum())
385
>>> print(len(matches))
450
>>> matches.sum() / float(len(matches))
np.float64(0.8555...)
我们看到,450 个预测中有超过 80% 与输入匹配。但是,还有其他更复杂的指标可用于判断分类器的性能:sklearn.metrics 子模块中提供了几个指标。
最有用的指标之一是 classification_report,它结合了几个度量并打印一个包含结果的表格。
>>> from sklearn import metrics
>>> print(metrics.classification_report(expected, predicted))
precision recall f1-score support
0 1.00 0.95 0.98 43
1 0.85 0.78 0.82 37
2 0.85 0.61 0.71 38
3 0.97 0.83 0.89 46
4 0.98 0.84 0.90 55
5 0.90 0.95 0.93 59
6 0.90 0.96 0.92 45
7 0.71 0.98 0.82 41
8 0.60 0.89 0.72 38
9 0.90 0.73 0.80 48
accuracy 0.86 450
macro avg 0.87 0.85 0.85 450
weighted avg 0.88 0.86 0.86 450
对于这种多标签分类,另一个有启发性的指标是混淆矩阵:它帮助我们可视化在分类错误中哪些标签正在被互换。
>>> print(metrics.confusion_matrix(expected, predicted))
[[41 0 0 0 0 1 0 1 0 0]
[ 0 29 2 0 0 0 0 0 4 2]
[ 0 2 23 0 0 0 1 0 12 0]
[ 0 0 1 38 0 1 0 0 5 1]
[ 0 0 0 0 46 0 2 7 0 0]
[ 0 0 0 0 0 56 1 1 0 1]
[ 0 0 0 0 1 1 43 0 0 0]
[ 0 0 0 0 0 1 0 40 0 0]
[ 0 2 0 0 0 0 0 2 34 0]
[ 0 1 1 1 0 2 1 5 2 35]]
我们在这里看到,特别是数字 1、2、3 和 9 经常被标记为 8。
3.4.4. 监督学习:房价数据的回归¶
在这里,我们将做一个回归问题的简短示例:从一组特征中学习一个连续值。
3.4.4.1. 快速浏览数据¶
我们将使用加州房价数据集,该数据集可在 scikit-learn 中获取。它记录了加州住房市场 8 个属性的测量值,以及中位数价格。问题是:给定新市场的属性,能否预测其价格?
>>> from sklearn.datasets import fetch_california_housing
>>> data = fetch_california_housing(as_frame=True)
>>> print(data.data.shape)
(20640, 8)
>>> print(data.target.shape)
(20640,)
我们可以看到,数据点略多于 20000 个。
DESCR 变量包含对数据集的详细描述。
>>> print(data.DESCR)
.. _california_housing_dataset:
California Housing dataset
--------------------------
**Data Set Characteristics:**
:Number of Instances: 20640
:Number of Attributes: 8 numeric, predictive attributes and the target
:Attribute Information:
- MedInc median income in block group
- HouseAge median house age in block group
- AveRooms average number of rooms per household
- AveBedrms average number of bedrooms per household
- Population block group population
- AveOccup average number of household members
- Latitude block group latitude
- Longitude block group longitude
:Missing Attribute Values: None
This dataset was obtained from the StatLib repository.
https://www.dcc.fc.up.pt/~ltorgo/Regression/cal_housing.html
The target variable is the median house value for California districts,
expressed in hundreds of thousands of dollars ($100,000).
This dataset was derived from the 1990 U.S. census, using one row per census
block group. A block group is the smallest geographical unit for which the U.S.
Census Bureau publishes sample data (a block group typically has a population
of 600 to 3,000 people).
A household is a group of people residing within a home. Since the average
number of rooms and bedrooms in this dataset are provided per household, these
columns may take surprisingly large values for block groups with few households
and many empty houses, such as vacation resorts.
It can be downloaded/loaded using the
:func:`sklearn.datasets.fetch_california_housing` function.
.. rubric:: References
- Pace, R. Kelley and Ronald Barry, Sparse Spatial Autoregressions,
Statistics and Probability Letters, 33 (1997) 291-297
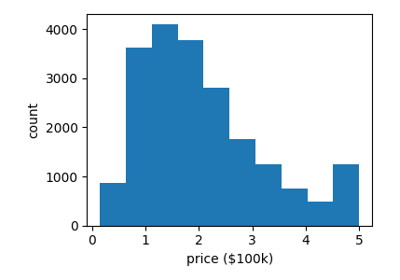
使用直方图、散点图或其他绘图类型快速可视化数据片段通常会有所帮助。使用 matplotlib,让我们显示目标值的直方图:每个街区的房价中位数。
>>> plt.hist(data.target)
(array([...

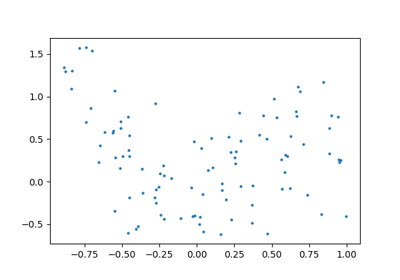
让我们快速查看一下,看看某些特征对于我们的问题是否比其他特征更相关。
>>> for index, feature_name in enumerate(data.feature_names):
... plt.figure()
... plt.scatter(data.data[feature_name], data.target)
<Figure size...
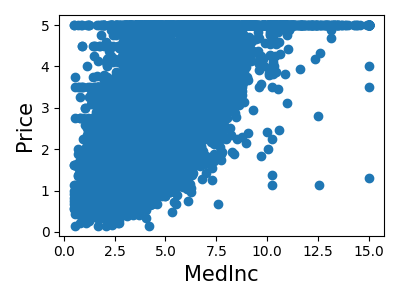
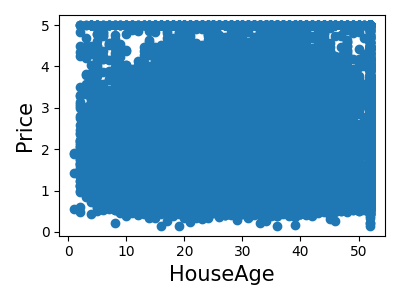
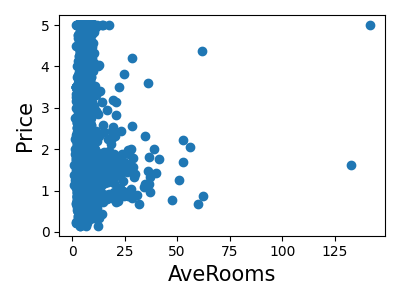
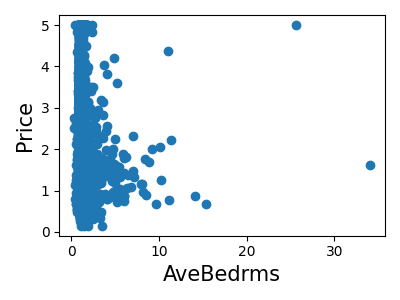
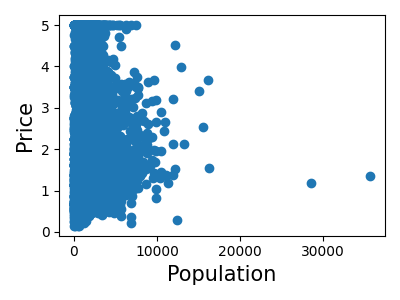
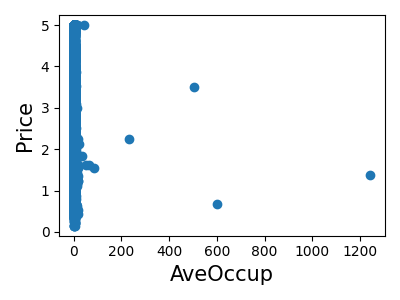
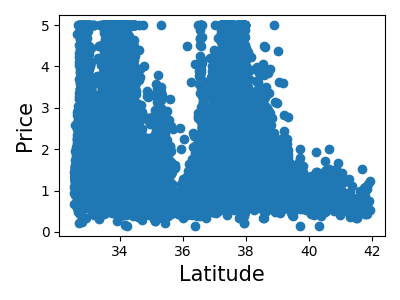
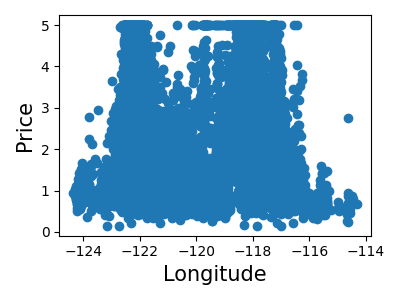
这是一种称为**特征选择**的技术的手动版本。
提示
有时,在机器学习中,使用特征选择来确定哪些特征对特定问题最有帮助非常有用。存在一些自动化方法可以量化这种选择信息量最大的特征的练习。
3.4.4.2. 预测房价:简单线性回归¶
现在我们将使用 scikit-learn 对房价数据执行简单的线性回归。可以使用多种回归器。一个特别简单的回归器是 LinearRegression:它基本上是普通最小二乘计算的包装器。
>>> from sklearn.model_selection import train_test_split
>>> X_train, X_test, y_train, y_test = train_test_split(data.data, data.target)
>>> from sklearn.linear_model import LinearRegression
>>> clf = LinearRegression()
>>> clf.fit(X_train, y_train)
LinearRegression()
>>> predicted = clf.predict(X_test)
>>> expected = y_test
>>> print("RMS: %s" % np.sqrt(np.mean((predicted - expected) ** 2)))
RMS: 0.7...
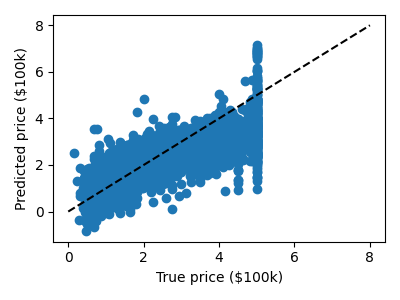
我们可以绘制误差:以预测值为函数的期望误差。
>>> plt.scatter(expected, predicted)
<matplotlib.collections.PathCollection object at ...>
提示
预测至少与真实价格相关,尽管显然存在一些偏差。我们可以想象通过计算真实价格和预测价格之间的 RMS 残差来评估回归器的性能。但是,这里有一些微妙之处,我们将在后面的章节中介绍。
3.4.5. 衡量预测性能¶
3.4.5.1. 对 K 近邻分类器的快速测试¶
在这里,我们将继续查看数字数据集,但我们将切换到 K 近邻分类器。K 近邻分类器是一种基于实例的分类器。K 近邻分类器根据参数空间中 *K* 个最近点的标签预测未知点的标签。
>>> # Get the data
>>> from sklearn.datasets import load_digits
>>> digits = load_digits()
>>> X = digits.data
>>> y = digits.target
>>> # Instantiate and train the classifier
>>> from sklearn.neighbors import KNeighborsClassifier
>>> clf = KNeighborsClassifier(n_neighbors=1)
>>> clf.fit(X, y)
KNeighborsClassifier(...)
>>> # Check the results using metrics
>>> from sklearn import metrics
>>> y_pred = clf.predict(X)
>>> print(metrics.confusion_matrix(y_pred, y))
[[178 0 0 0 0 0 0 0 0 0]
[ 0 182 0 0 0 0 0 0 0 0]
[ 0 0 177 0 0 0 0 0 0 0]
[ 0 0 0 183 0 0 0 0 0 0]
[ 0 0 0 0 181 0 0 0 0 0]
[ 0 0 0 0 0 182 0 0 0 0]
[ 0 0 0 0 0 0 181 0 0 0]
[ 0 0 0 0 0 0 0 179 0 0]
[ 0 0 0 0 0 0 0 0 174 0]
[ 0 0 0 0 0 0 0 0 0 180]]
显然,我们找到了一个完美的分类器!但由于我们之前看到的原因,这是具有误导性的:分类器本质上“记住”了它已经看到的所有样本。要真正测试此算法的性能,我们需要尝试一些它*尚未*见过的样本。
回归模型也会出现此问题。在下面,我们将一个名为“决策树”的其他基于实例的模型拟合到我们之前介绍的加州房价数据集。
>>> from sklearn.datasets import fetch_california_housing
>>> from sklearn.tree import DecisionTreeRegressor
>>> data = fetch_california_housing(as_frame=True)
>>> clf = DecisionTreeRegressor().fit(data.data, data.target)
>>> predicted = clf.predict(data.data)
>>> expected = data.target
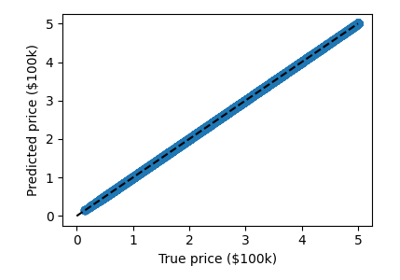
>>> plt.scatter(expected, predicted)
<matplotlib.collections.PathCollection object at ...>
>>> plt.plot([0, 50], [0, 50], '--k')
[<matplotlib.lines.Line2D object at ...]
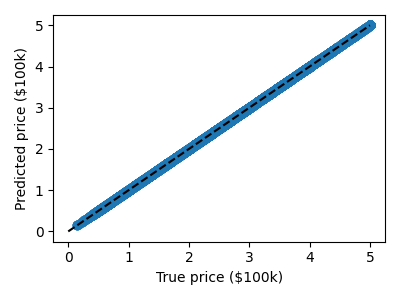
在这里,预测似乎也完美无缺,因为模型能够完美地记住训练集。
警告
测试集上的性能
测试集上的性能不会衡量过拟合(如上所述)。
3.4.5.2. 正确的方法:使用验证集¶
学习预测函数的参数并在相同的数据上对其进行测试是一种方法论上的错误:一个仅仅重复其刚刚看到的样本标签的模型将具有完美的得分,但无法对尚未见过的任何数据进行有用的预测。
为了避免过拟合,我们必须定义两个不同的集合。
训练集 X_train、y_train 用于学习预测模型的参数。
测试集 X_test、y_test 用于评估拟合的预测模型。
在 scikit-learn 中,可以使用 train_test_split() 函数快速计算此类随机拆分。
>>> from sklearn import model_selection
>>> X = digits.data
>>> y = digits.target
>>> X_train, X_test, y_train, y_test = model_selection.train_test_split(X, y,
... test_size=0.25, random_state=0)
>>> print("%r, %r, %r" % (X.shape, X_train.shape, X_test.shape))
(1797, 64), (1347, 64), (450, 64)
现在我们在训练数据上进行训练,在测试数据上进行测试。
>>> clf = KNeighborsClassifier(n_neighbors=1).fit(X_train, y_train)
>>> y_pred = clf.predict(X_test)
>>> print(metrics.confusion_matrix(y_test, y_pred))
[[37 0 0 0 0 0 0 0 0 0]
[ 0 43 0 0 0 0 0 0 0 0]
[ 0 0 43 1 0 0 0 0 0 0]
[ 0 0 0 45 0 0 0 0 0 0]
[ 0 0 0 0 38 0 0 0 0 0]
[ 0 0 0 0 0 47 0 0 0 1]
[ 0 0 0 0 0 0 52 0 0 0]
[ 0 0 0 0 0 0 0 48 0 0]
[ 0 0 0 0 0 0 0 0 48 0]
[ 0 0 0 1 0 1 0 0 0 45]]
>>> print(metrics.classification_report(y_test, y_pred))
precision recall f1-score support
0 1.00 1.00 1.00 37
1 1.00 1.00 1.00 43
2 1.00 0.98 0.99 44
3 0.96 1.00 0.98 45
4 1.00 1.00 1.00 38
5 0.98 0.98 0.98 48
6 1.00 1.00 1.00 52
7 1.00 1.00 1.00 48
8 1.00 1.00 1.00 48
9 0.98 0.96 0.97 47
accuracy 0.99 450
macro avg 0.99 0.99 0.99 450
weighted avg 0.99 0.99 0.99 450
平均 f1 分数通常用作算法整体性能的便捷度量。它出现在分类报告的底行;也可以直接访问它。
>>> metrics.f1_score(y_test, y_pred, average="macro")
np.float64(0.991367...)
我们之前看到的过拟合可以通过计算训练数据本身的 f1 分数来量化。
>>> metrics.f1_score(y_train, clf.predict(X_train), average="macro")
np.float64(1.0)
注意
回归指标在回归模型的情况下,我们需要使用不同的指标,例如解释方差。
3.4.5.3. 通过验证进行模型选择¶
提示
我们已将高斯朴素贝叶斯、支持向量机和 K 近邻分类器应用于数字数据集。现在我们已经有了这些验证工具,我们可以定量地询问这三个估计器中哪一个最适合此数据集。
使用每个估计器的默认超参数,哪个在**验证集**上提供了最佳的 f1 分数?回想一下,超参数是在实例化分类器时设置的参数:例如,
KNeighborsClassifier(n_neighbors=1)中的n_neighbors。>>> from sklearn.naive_bayes import GaussianNB >>> from sklearn.neighbors import KNeighborsClassifier >>> from sklearn.svm import LinearSVC >>> X = digits.data >>> y = digits.target >>> X_train, X_test, y_train, y_test = model_selection.train_test_split(X, y, ... test_size=0.25, random_state=0) >>> for Model in [GaussianNB(), KNeighborsClassifier(), LinearSVC(dual=False)]: ... clf = Model.fit(X_train, y_train) ... y_pred = clf.predict(X_test) ... print('%s: %s' % ... (Model.__class__.__name__, metrics.f1_score(y_test, y_pred, average="macro"))) GaussianNB: 0.8... KNeighborsClassifier: 0.9... LinearSVC: 0.9...
对于每个分类器,哪个超参数值对数字数据提供了最佳结果?对于
LinearSVC,使用loss='l2'和loss='l1'。对于KNeighborsClassifier,我们使用介于 1 和 10 之间的n_neighbors。请注意,GaussianNB没有可调整的超参数。LinearSVC(loss='l1'): 0.930570687535 LinearSVC(loss='l2'): 0.933068826918 ------------------- KNeighbors(n_neighbors=1): 0.991367521884 KNeighbors(n_neighbors=2): 0.984844206884 KNeighbors(n_neighbors=3): 0.986775344954 KNeighbors(n_neighbors=4): 0.980371905382 KNeighbors(n_neighbors=5): 0.980456280495 KNeighbors(n_neighbors=6): 0.975792419414 KNeighbors(n_neighbors=7): 0.978064579214 KNeighbors(n_neighbors=8): 0.978064579214 KNeighbors(n_neighbors=9): 0.978064579214 KNeighbors(n_neighbors=10): 0.975555089773
解决方案:代码来源
3.4.5.4. 交叉验证¶
交叉验证包括反复将数据拆分为训练集和测试集对,称为“折叠”。Scikit-learn 带有一个函数来自动计算所有这些折叠上的分数。在这里,我们使用 k=5 进行 KFold。
>>> clf = KNeighborsClassifier()
>>> from sklearn.model_selection import cross_val_score
>>> cross_val_score(clf, X, y, cv=5)
array([0.947..., 0.955..., 0.966..., 0.980..., 0.963... ])
我们可以使用不同的拆分策略,例如随机拆分。
>>> from sklearn.model_selection import ShuffleSplit
>>> cv = ShuffleSplit(n_splits=5)
>>> cross_val_score(clf, X, y, cv=cv)
array([...])
提示
scikit-learn 中存在 许多不同的交叉验证策略。它们通常用于考虑非独立同分布数据集。
3.4.5.5. 使用交叉验证进行超参数优化¶
考虑正则化线性模型,例如使用 l2 正则化的*岭回归*和使用 l1 正则化的*套索回归*。选择它们的正则化参数非常重要。
让我们在糖尿病数据集上设置这些参数,这是一个简单的回归问题。糖尿病数据包含在 442 名患者身上测量的 10 个生理变量(年龄、性别、体重、血压),以及一年后疾病进展的指示。
>>> from sklearn.datasets import load_diabetes
>>> data = load_diabetes()
>>> X, y = data.data, data.target
>>> print(X.shape)
(442, 10)
使用默认超参数:我们计算交叉验证分数。
>>> from sklearn.linear_model import Ridge, Lasso
>>> for Model in [Ridge, Lasso]:
... model = Model()
... print('%s: %s' % (Model.__name__, cross_val_score(model, X, y).mean()))
Ridge: 0.4...
Lasso: 0.3...
基本超参数优化¶
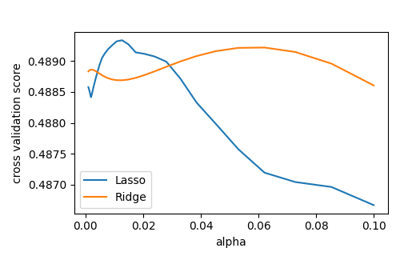
我们计算交叉验证分数作为 alpha 的函数,alpha 是 Lasso 和 Ridge 正则化强度的参数。我们选择介于 0.0001 和 1 之间的 20 个 alpha 值。
>>> alphas = np.logspace(-3, -1, 30)
>>> for Model in [Lasso, Ridge]:
... scores = [cross_val_score(Model(alpha), X, y, cv=3).mean()
... for alpha in alphas]
... plt.plot(alphas, scores, label=Model.__name__)
[<matplotlib.lines.Line2D object at ...
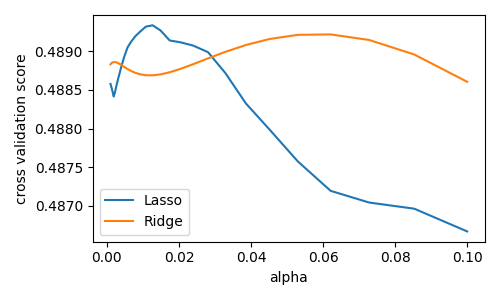
自动执行网格搜索¶
sklearn.grid_search.GridSearchCV 由估计器以及要搜索的参数值字典构造。我们可以通过这种方式找到最佳参数。
>>> from sklearn.model_selection import GridSearchCV
>>> for Model in [Ridge, Lasso]:
... gscv = GridSearchCV(Model(), dict(alpha=alphas), cv=3).fit(X, y)
... print('%s: %s' % (Model.__name__, gscv.best_params_))
Ridge: {'alpha': np.float64(0.06210169418915616)}
Lasso: {'alpha': np.float64(0.01268961003167922)}
内置超参数搜索¶
对于 scikit-learn 中的一些模型,可以在大型数据集上更有效地执行交叉验证。在这种情况下,包含了特定模型的交叉验证版本。 的交叉验证版本Ridge 和 Lasso 分别是 RidgeCV 和 LassoCV。可以如下执行这些估计器的参数搜索
>>> from sklearn.linear_model import RidgeCV, LassoCV
>>> for Model in [RidgeCV, LassoCV]:
... model = Model(alphas=alphas, cv=3).fit(X, y)
... print('%s: %s' % (Model.__name__, model.alpha_))
RidgeCV: 0.0621016941892
LassoCV: 0.0126896100317
我们看到结果与 GridSearchCV 返回的结果一致。
嵌套交叉验证¶
我们如何衡量这些估计器的性能?我们已经使用数据来设置超参数,因此我们需要在实际的新数据上进行测试。我们可以通过在我们的 CV 对象上运行 cross_val_score() 来做到这一点。这里有两个交叉验证循环正在进行,这被称为“嵌套交叉验证”。
for Model in [RidgeCV, LassoCV]:
scores = cross_val_score(Model(alphas=alphas, cv=3), X, y, cv=3)
print(Model.__name__, np.mean(scores))
3.4.6. 无监督学习:降维和可视化¶
无监督学习应用于没有 y 的 X:没有标签的数据。一个典型的用例是在数据中找到隐藏的结构。
3.4.6.1. 降维:PCA¶
降维推导出比原始特征集更小的一组新的人工特征。这里我们将使用 主成分分析 (PCA),这是一种努力保留原始数据大部分方差的降维方法。我们将使用 sklearn.decomposition.PCA 在 iris 数据集上。
>>> X = iris.data
>>> y = iris.target
提示
PCA 使用矩阵 X 的截断奇异值分解来计算原始特征的线性组合,以将数据投影到前几个奇异向量组成的基上。
>>> from sklearn.decomposition import PCA
>>> pca = PCA(n_components=2, whiten=True)
>>> pca.fit(X)
PCA(n_components=2, whiten=True)
拟合后,PCA 在 components_ 属性中公开奇异向量。
>>> pca.components_
array([[ 0.3..., -0.08..., 0.85..., 0.3...],
[ 0.6..., 0.7..., -0.1..., -0.07...]])
其他属性也可用。
>>> pca.explained_variance_ratio_
array([0.92..., 0.053...])
让我们沿着前两个维度投影 iris 数据集:
>>> X_pca = pca.transform(X)
>>> X_pca.shape
(150, 2)
PCA normalizes 和 whitens 数据,这意味着数据现在在两个分量上都以单位方差为中心。
>>> X_pca.mean(axis=0)
array([...e-15, ...e-15])
>>> X_pca.std(axis=0, ddof=1)
array([1., 1.])
此外,样本分量不再具有任何线性相关性。
>>> np.corrcoef(X_pca.T)
array([[1.00000000e+00, 0.0],
[0.0, 1.00000000e+00]])
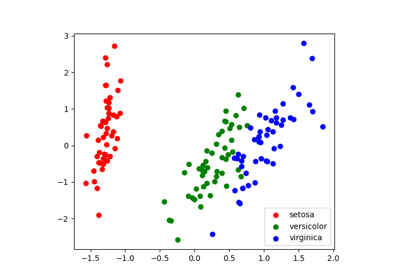
保留 2 或 3 个分量,PCA 可用于可视化数据集。
>>> target_ids = range(len(iris.target_names))
>>> for i, c, label in zip(target_ids, 'rgbcmykw', iris.target_names):
... plt.scatter(X_pca[y == i, 0], X_pca[y == i, 1],
... c=c, label=label)
<matplotlib.collections.PathCollection ...
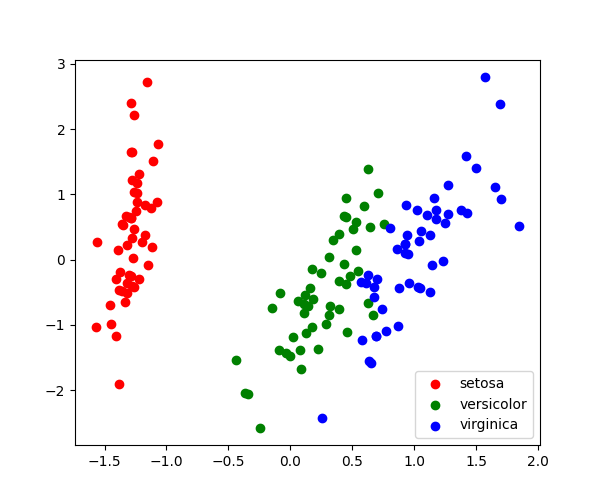
提示
请注意,此投影是在**没有**任何关于标签(由颜色表示)的信息的情况下确定的:这就是学习是**无监督**的意义所在。尽管如此,我们看到投影使我们能够深入了解参数空间中不同花的分布:特别地,iris setosa 比其他两种物种更具区别性。
3.4.6.2. 使用非线性嵌入的可视化:tSNE¶
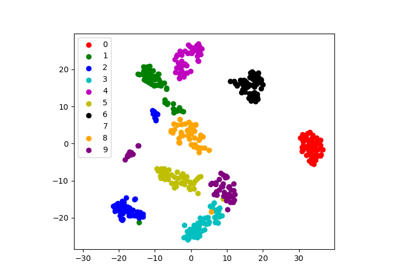
对于可视化,更复杂的嵌入可能有用(对于统计分析,它们更难以控制)。sklearn.manifold.TSNE 就是这样一种强大的流形学习方法。我们将其应用于digits数据集,因为数字是维度为 8*8 = 64 的向量。将它们嵌入到 2D 中可以实现可视化。
>>> # Take the first 500 data points: it's hard to see 1500 points
>>> X = digits.data[:500]
>>> y = digits.target[:500]
>>> # Fit and transform with a TSNE
>>> from sklearn.manifold import TSNE
>>> tsne = TSNE(n_components=2, learning_rate='auto', init='random', random_state=0)
>>> X_2d = tsne.fit_transform(X)
>>> # Visualize the data
>>> plt.scatter(X_2d[:, 0], X_2d[:, 1], c=y)
<matplotlib.collections.PathCollection object at ...>
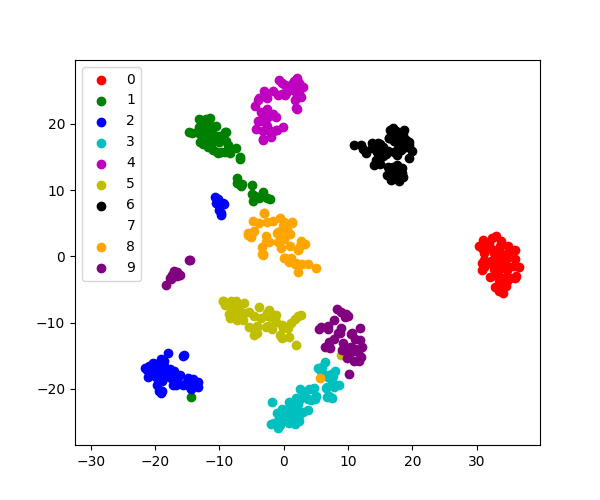
sklearn.manifold.TSNE 很好地分离了不同类别的数字,即使它没有访问类信息。
3.4.7. 参数选择、验证和测试¶
3.4.7.1. 超参数、过拟合和欠拟合¶
另请参阅
与验证和交叉验证相关的问题是机器学习实践中最重要的方面之一。为您的数据选择最佳模型至关重要,并且是机器学习实践者通常不重视的问题的一部分。
核心问题是:**如果我们的估计器性能不佳,我们应该如何前进?**
使用更简单或更复杂的模型?
为每个观察到的数据点添加更多特征?
添加更多训练样本?
答案通常违反直觉。特别是,**有时使用更复杂的模型会导致更差的结果。** 此外,**有时添加训练数据不会改善您的结果。** 能够确定哪些步骤可以改进您的模型,是成功的机器学习实践者与不成功的机器学习实践者之间的区别。
偏差-方差权衡:在简单回归问题上的说明¶
让我们从一个简单的 1D 回归问题开始。这将帮助我们轻松地可视化数据和模型,并且结果很容易推广到更高维的数据集。我们将探索一个简单的**线性回归**问题,使用 sklearn.linear_model。
X = np.c_[0.5, 1].T
y = [0.5, 1]
X_test = np.c_[0, 2].T
在没有噪声的情况下,线性回归完美地拟合数据。
from sklearn import linear_model
regr = linear_model.LinearRegression()
regr.fit(X, y)
plt.plot(X, y, "o")
plt.plot(X_test, regr.predict(X_test))
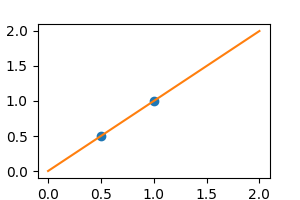
[<matplotlib.lines.Line2D object at 0x7f78e6f06510>]
在现实生活中,我们的数据中存在噪声(例如测量噪声)。
rng = np.random.default_rng(27446968)
for _ in range(6):
noisy_X = X + np.random.normal(loc=0, scale=0.1, size=X.shape)
plt.plot(noisy_X, y, "o")
regr.fit(noisy_X, y)
plt.plot(X_test, regr.predict(X_test))
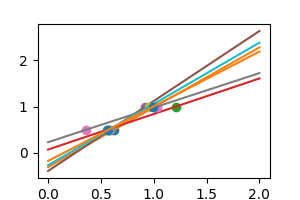
如我们所见,我们的线性模型捕获并放大了数据中的噪声。它显示出很大的方差。
我们可以使用另一个使用正则化的线性估计器,即 Ridge 估计器。该估计器通过将系数缩小到零来正则化系数,假设非常高的相关性通常是虚假的。alpha 参数控制使用的收缩量。
regr = linear_model.Ridge(alpha=0.1)
np.random.seed(0)
for _ in range(6):
noisy_X = X + np.random.normal(loc=0, scale=0.1, size=X.shape)
plt.plot(noisy_X, y, "o")
regr.fit(noisy_X, y)
plt.plot(X_test, regr.predict(X_test))
plt.show()
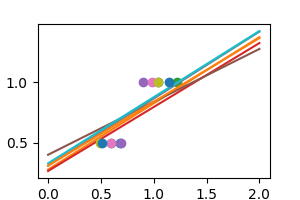
如我们所见,估计器显示出更小的方差。但是它系统地低估了系数。它显示出偏差行为。
这是一个典型的**偏差/方差权衡**示例:非正则化估计器没有偏差,但它们可以显示出很大的方差。高度正则化的模型方差小,但偏差高。这种偏差不一定是坏事:重要的是选择偏差和方差之间的权衡,从而获得最佳预测性能。对于特定数据集,存在一个最佳点,对应于数据可以支持的最高复杂度,具体取决于可用噪声和观测值的量。
3.4.7.2. 可视化偏差/方差权衡¶
提示
给定一个特定的数据集和一个模型(例如多项式),我们希望了解偏差(欠拟合)或方差是否限制了预测,以及如何调整超参数(这里为 d,多项式的次数)以获得最佳拟合。
在给定数据上,让我们拟合一个具有不同次数的简单多项式回归模型。
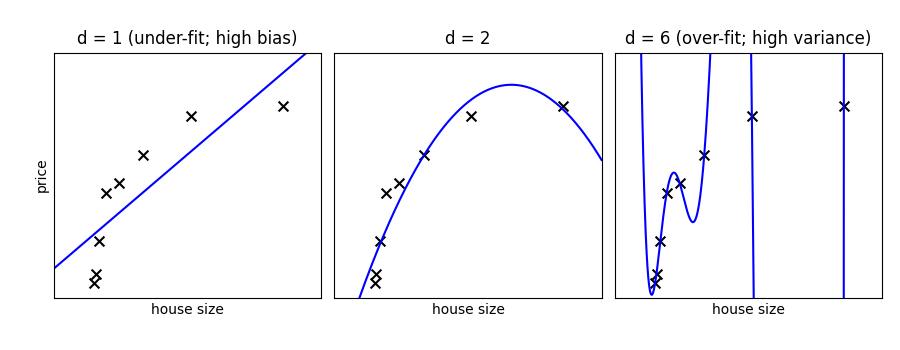
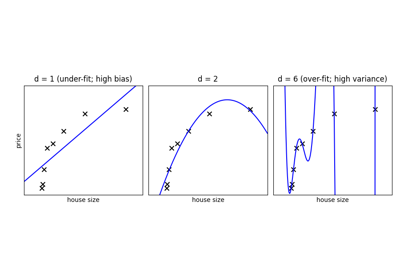
提示
在上图中,我们看到了三个不同d值的拟合结果。对于d = 1,数据拟合不足。这意味着模型过于简单:没有任何直线能很好地拟合这些数据。在这种情况下,我们说模型存在高偏差。模型本身是有偏差的,这将反映在数据拟合不良的事实上。在另一个极端,对于d = 6,数据过拟合。这意味着模型有太多自由参数(在这种情况下为 6 个),可以调整这些参数以完美拟合训练数据。但是,如果我们在此图中添加一个新点,则该点很可能离表示 6 次拟合的曲线很远。在这种情况下,我们说模型存在高方差。术语“高方差”的原因是,如果任何输入点发生轻微变化,都可能导致非常不同的模型。
在中间,对于d = 2,我们找到了一个良好的中间点。它相当好地拟合了数据,并且没有出现两侧图形中看到的偏差和方差问题。我们希望有一种方法能够定量地识别偏差和方差,并优化元参数(在本例中为多项式次数 d),以确定最佳算法。
验证曲线¶
让我们创建一个类似于上面示例的数据集。
>>> def generating_func(x, rng, err=0.5):
... return rng.normal(10 - 1. / (x + 0.1), err)
>>> # randomly sample more data
>>> rng = np.random.default_rng(27446968)
>>> x = rng.random(size=200)
>>> y = generating_func(x, err=1., rng=rng)

量化模型偏差和方差的核心是将其应用于测试数据,这些数据是从与训练数据相同的分布中采样而来,但会捕获独立的噪声。
>>> xtrain, xtest, ytrain, ytest = train_test_split(x, y, test_size=0.4)
验证曲线 验证曲线包括改变控制模型复杂度的模型参数(此处为多项式的次数),并测量模型在训练数据和测试数据上的误差(例如使用交叉验证)。然后调整模型参数以使测试误差最小化。
我们使用sklearn.model_selection.validation_curve()计算训练和测试误差,并将其绘制出来。
>>> from sklearn.model_selection import validation_curve
>>> degrees = np.arange(1, 21)
>>> model = make_pipeline(PolynomialFeatures(), LinearRegression())
>>> # Vary the "degrees" on the pipeline step "polynomialfeatures"
>>> train_scores, validation_scores = validation_curve(
... model, x[:, np.newaxis], y,
... param_name='polynomialfeatures__degree',
... param_range=degrees)
>>> # Plot the mean train score and validation score across folds
>>> plt.plot(degrees, validation_scores.mean(axis=1), label='cross-validation')
[<matplotlib.lines.Line2D object at ...>]
>>> plt.plot(degrees, train_scores.mean(axis=1), label='training')
[<matplotlib.lines.Line2D object at ...>]
>>> plt.legend(loc='best')
<matplotlib.legend.Legend object at ...>
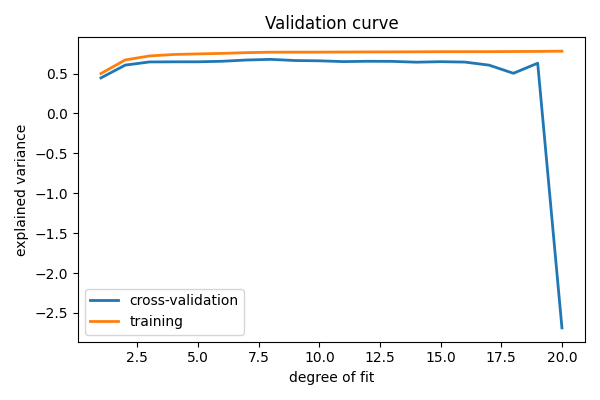
此图显示了为什么验证很重要。在图的左侧,我们有非常低次的多项式,它对数据拟合不足。这导致训练集和验证集的解释方差都较低。在图的最右侧,我们有一个非常高次的多项式,它对数据过拟合。这可以从训练解释方差非常高的事实中看出,而在验证集上,它很低。选择d约为 4 或 5 可以获得最佳权衡。
提示
敏锐的读者会意识到这里有些问题:在上图中,d = 4给出了最佳结果。但在前面的图中,我们发现d = 6极大地过拟合了数据。这里发生了什么?区别在于所使用的训练点数。在前面的示例中,只有八个训练点。在本例中,我们有 100 个。作为一般的经验法则,使用的训练点越多,可以使用越复杂的模型。但是,如何确定对于给定模型,更多的训练点是否有用?学习曲线对此很有帮助。
学习曲线¶
学习曲线显示了训练和验证分数作为训练点数的函数。请注意,当我们在训练数据的一个子集上进行训练时,训练分数是使用此子集计算的,而不是使用完整的训练集。此曲线定量地说明了添加训练样本是否有益。
scikit-learn提供了sklearn.model_selection.learning_curve()
>>> from sklearn.model_selection import learning_curve
>>> train_sizes, train_scores, validation_scores = learning_curve(
... model, x[:, np.newaxis], y, train_sizes=np.logspace(-1, 0, 20))
>>> # Plot the mean train score and validation score across folds
>>> plt.plot(train_sizes, validation_scores.mean(axis=1), label='cross-validation')
[<matplotlib.lines.Line2D object at ...>]
>>> plt.plot(train_sizes, train_scores.mean(axis=1), label='training')
[<matplotlib.lines.Line2D object at ...>]
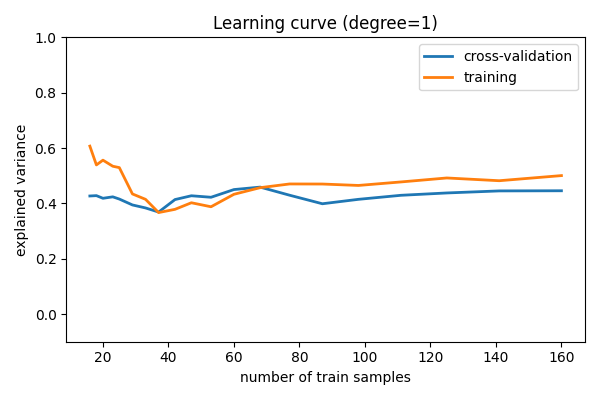
对于degree=1模型¶
请注意,验证分数随着训练集的增大通常会增加,而训练分数随着训练集的增大通常会减少。随着训练规模的增加,它们将收敛到一个单一的值。
从上面的讨论中,我们知道d = 1是一个高偏差估计量,它对数据拟合不足。这由训练和验证分数都较低的事实表明。当遇到这种类型的学习曲线时,我们可以预期添加更多训练数据将无济于事:两条线都收敛到一个相对较低的分数。
当学习曲线收敛到一个低分时,我们有一个高偏差模型。
高偏差模型可以通过以下方式改进:
使用更复杂的模型(即在本例中,增加
d)。为每个样本收集更多特征。
减少正则化模型中的正则化。
然而,增加样本数量并不能改进高偏差模型。
现在让我们看看一个高方差(即过拟合)模型。
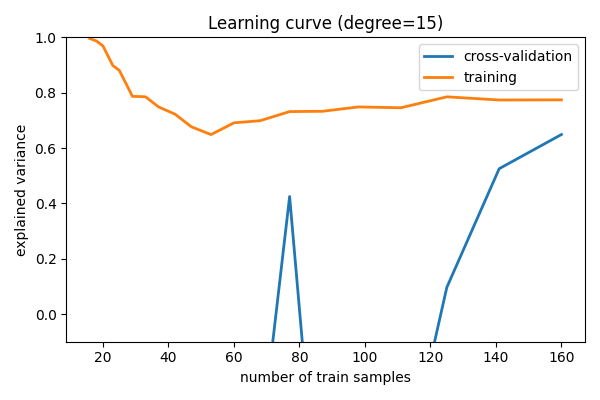
对于degree=15模型¶
这里我们显示了d = 15的学习曲线。从上面的讨论中,我们知道d = 15是一个高方差估计量,它过拟合了数据。这由训练分数远高于验证分数的事实表明。当我们向此训练集添加更多样本时,训练分数将继续下降,而交叉验证误差将继续增加,直到它们在中间相遇。
尚未使用完整训练集收敛的学习曲线表示高方差、过拟合模型。
高方差模型可以通过以下方式改进:
收集更多训练样本。
使用不太复杂的模型(即在本例中,使
d更小)。增加正则化。
特别是,为每个样本收集更多特征不会帮助结果。
3.4.7.3. 模型选择总结¶
我们上面已经看到,算法性能不佳可能是由于两种可能的情况造成的:高偏差(欠拟合)和高方差(过拟合)。为了评估我们的算法,我们将一部分训练数据留作交叉验证。使用学习曲线技术,我们可以在数据越来越大的子集上进行训练,评估训练误差和交叉验证误差,以确定我们的算法是否存在高方差或高偏差。但是我们如何处理这些信息呢?
高偏差¶
如果模型显示出高偏差,以下操作可能会有所帮助:
添加更多特征。在我们预测房价的示例中,利用房屋所在社区、房屋建造年份、地块大小等信息可能会有所帮助。将这些特征添加到训练集和测试集中可以改进高偏差估计量。
使用更复杂的模型。增加模型的复杂性可以帮助改善偏差。对于多项式拟合,可以通过增加次数 d 来实现。每种学习技术都有自己的增加复杂度的方法。
使用较少的样本。虽然这不会提高分类效果,但高偏差算法可以用较小的训练样本获得几乎相同的误差。对于计算量大的算法,减少训练样本量可以极大地提高速度。
减少正则化。正则化是一种用于在某些机器学习模型中强加简单性的技术,方法是添加一个取决于参数特征的惩罚项。如果模型具有高偏差,减少正则化的影响可以带来更好的结果。
高方差¶
如果模型显示出高方差,以下操作可能会有所帮助:
使用较少的特征。使用特征选择技术可能会有用,并减少估计量的过拟合。
使用更简单的模型。模型复杂性和过拟合密不可分。
使用更多训练样本。添加训练样本可以减少过拟合的影响,并导致高方差估计量的改进。
增加正则化。正则化旨在防止过拟合。在高方差模型中,增加正则化可以带来更好的结果。
这些选择在现实世界中变得非常重要。例如,由于望远镜时间有限,天文学家必须在观测大量物体和观测每个物体的众多特征之间寻求平衡。确定哪种对于特定学习任务更重要可以为天文学家采用的观测策略提供信息。
3.4.7.4. 最后一句忠告:分离验证集和测试集¶
使用验证方案确定超参数意味着我们正在将超参数拟合到特定的验证集。就像参数可以过度拟合到训练集一样,超参数也可以过度拟合到验证集。因此,验证误差往往会低估新数据的分类误差。
因此,建议将数据分成三个集合:
训练集,用于训练模型(通常占数据约 60%)。
验证集,用于验证模型(通常占数据约 20%)。
测试集,用于评估经过验证的模型的预期误差(通常占数据约 20%)。
许多机器学习从业者不分离测试集和验证集。但是,如果您的目标是评估模型在未知数据上的误差,则使用独立的测试集至关重要。