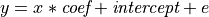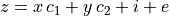3.1. Python 中的统计学

作者: Gaël Varoquaux

需求

• 标准科学 Python 环境（NumPy、SciPy、matplotlib）

• Pandas

• Statsmodels

• Seaborn

要安装 Python 和这些依赖项，建议您下载 Anaconda Python，或者最好在 Ubuntu 或其他 Linux 系统下使用包管理器。

另请参阅

• Python 中的贝叶斯统计学: 本章不涵盖贝叶斯统计学的工具。对于贝叶斯建模特别感兴趣的是 PyMC，它在 Python 中实现了概率编程语言。

• 阅读统计学书籍: Think stats 书籍可以免费获得 PDF 或印刷版，是统计学的入门书籍。

小贴士

为什么选择 Python 进行统计学分析？

R 是一种专门用于统计学的语言。Python 是一种通用语言，具有统计模块。R 比 Python 拥有更多统计分析功能，并具有专门的语法。但是，当涉及构建将统计学与例如图像分析、文本挖掘或物理实验控制相结合的复杂分析管道时，Python 的丰富性将成为一项宝贵的资产。

小贴士

在本文档中，Python 输入用符号“>>>”表示。

免责声明：性别问题

本教程中的一些示例是围绕性别问题选择的。原因是，对于这类问题，控制主张的真实性对许多人来说确实很重要。

3.1.1. 数据表示和交互

3.1.1.1. 数据作为表格

我们考虑用于统计分析的设置是，由一组不同的属性或特征描述的多个观察或样本。然后可以将数据视为一个二维表格或矩阵，其中列表示数据的不同属性，行表示观察结果。例如，包含在 examples/brain_size.csv 中的数据

"";"Gender";"FSIQ";"VIQ";"PIQ";"Weight";"Height";"MRI_Count"
"1";"Female";133;132;124;"118";"64.5";816932
"2";"Male";140;150;124;".";"72.5";1001121
"3";"Male";139;123;150;"143";"73.3";1038437
"4";"Male";133;129;128;"172";"68.8";965353
"5";"Female";137;132;134;"147";"65.0";951545

3.1.1.2. Pandas 数据框

小贴士

我们将使用 pandas.DataFrame（来自 pandas 模块）来存储和操作此数据。它是电子表格的 Python 等价物。它不同于二维 numpy 数组，因为它具有命名的列，可以按列包含混合的数据类型，并具有详细的选择和枢轴机制。

创建数据框：读取数据文件或转换数组

分隔符

这是一个 CSV 文件，但分隔符是“;”。

从 CSV 文件读取：使用上面的 CSV 文件，该文件提供了大脑大小、重量和智商（Willerman 等人，1991 年）的观察结果，数据是数值和分类值的混合。

>>> import pandas
>>> data = pandas.read_csv('examples/brain_size.csv', sep=';', na_values=".")
>>> data
    Unnamed: 0  Gender  FSIQ  VIQ  PIQ  Weight  Height  MRI_Count
0            1  Female   133  132  124   118.0    64.5     816932
1            2    Male   140  150  124     NaN    72.5    1001121
2            3    Male   139  123  150   143.0    73.3    1038437
3            4    Male   133  129  128   172.0    68.8     965353
4            5  Female   137  132  134   147.0    65.0     951545
...

警告

缺失值

CSV 文件中第二个个体的体重缺失。如果我们没有指定缺失值（NA = 不可用）标记，我们将无法进行统计分析。

从数组创建：pandas.DataFrame 也可以被视为一维“系列”的字典，例如数组或列表。如果我们有 3 个 numpy 数组

>>> import numpy as np
>>> t = np.linspace(-6, 6, 20)
>>> sin_t = np.sin(t)
>>> cos_t = np.cos(t)

我们可以将它们公开为 pandas.DataFrame

>>> pandas.DataFrame({'t': t, 'sin': sin_t, 'cos': cos_t})
           t       sin       cos
0  -6.000000  0.279415  0.960170
1  -5.368421  0.792419  0.609977
2  -4.736842  0.999701  0.024451
3  -4.105263  0.821291 -0.570509
4  -3.473684  0.326021 -0.945363
5  -2.842105 -0.295030 -0.955488
6  -2.210526 -0.802257 -0.596979
7  -1.578947 -0.999967 -0.008151
8  -0.947368 -0.811882  0.583822
...

其他输入：pandas 可以从 SQL、excel 文件或其他格式输入数据。请参见 pandas 文档。

操作数据

data 是一个 pandas.DataFrame，类似于 R 的数据框。

>>> data.shape    # 40 rows and 8 columns
(40, 8)

>>> data.columns  # It has columns
Index(['Unnamed: 0', 'Gender', 'FSIQ', 'VIQ', 'PIQ', 'Weight', 'Height',
       'MRI_Count'],
      dtype='object')

>>> print(data['Gender'])  # Columns can be addressed by name
0     Female
1       Male
2       Male
3       Male
4     Female
...

>>> # Simpler selector
>>> data[data['Gender'] == 'Female']['VIQ'].mean()
np.float64(109.45)

注意

要快速查看大型数据框，请使用其 describe 方法：pandas.DataFrame.describe()。

groupby：根据分类变量的值拆分数据框。

>>> groupby_gender = data.groupby('Gender')
>>> for gender, value in groupby_gender['VIQ']:
...     print((gender, value.mean()))
('Female', np.float64(109.45))
('Male', np.float64(115.25))

groupby_gender 是一个功能强大的对象，它公开了对结果数据框组的许多操作。

>>> groupby_gender.mean()
        Unnamed: 0   FSIQ     VIQ     PIQ      Weight     Height  MRI_Count
Gender
Female       19.65  111.9  109.45  110.45  137.200000  65.765000   862654.6
Male         21.35  115.0  115.25  111.60  166.444444  71.431579   954855.4

小贴士

在 groupby_gender 上使用制表符自动完成以查找更多信息。其他常见的分组函数是中位数、计数（用于检查不同子集中缺失值的数量）或求和。GroupBy 评估是惰性的，在应用聚合函数之前不会执行任何操作。

练习

• 整个群体的 VIQ 的平均值是多少？

• 本研究中包含多少男性/女性？

  提示 使用“制表符自动完成”找出可以调用的方法，而不是上面的示例中的“平均值”。

• 男性和女性的 MRI 计数以对数单位表示的平均值是多少？

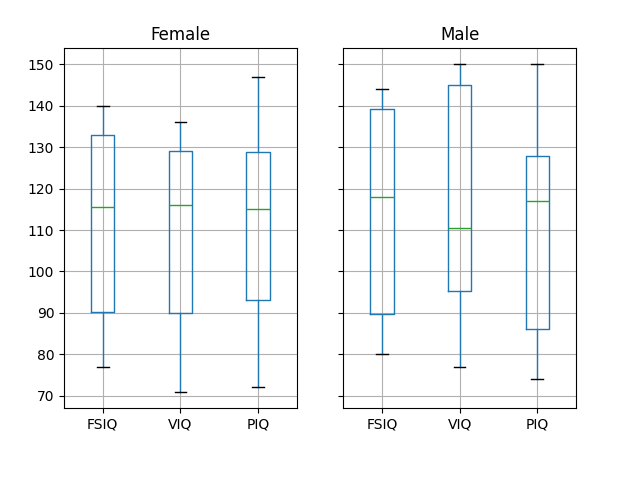
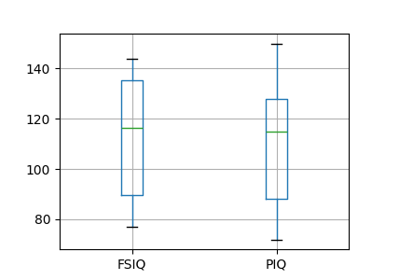
注意

groupby_gender.boxplot 用于上面的绘图（请参见 此示例）。

绘制数据

Pandas 附带一些绘图工具（pandas.plotting，在幕后使用 matplotlib）来显示数据框中数据的统计信息。

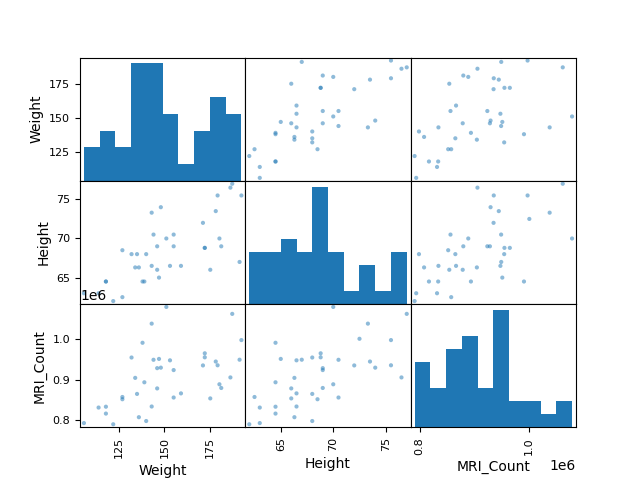
散点矩阵:

>>> from pandas import plotting
>>> plotting.scatter_matrix(data[['Weight', 'Height', 'MRI_Count']])
array([[<Axes: xlabel='Weight', ylabel='Weight'>,
        <Axes: xlabel='Height', ylabel='Weight'>,
        <Axes: xlabel='MRI_Count', ylabel='Weight'>],
       [<Axes: xlabel='Weight', ylabel='Height'>,
        <Axes: xlabel='Height', ylabel='Height'>,
        <Axes: xlabel='MRI_Count', ylabel='Height'>],
       [<Axes: xlabel='Weight', ylabel='MRI_Count'>,
        <Axes: xlabel='Height', ylabel='MRI_Count'>,
        <Axes: xlabel='MRI_Count', ylabel='MRI_Count'>]], dtype=object)

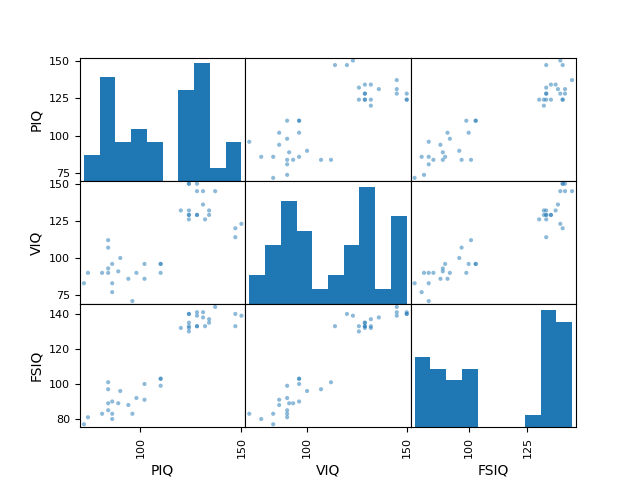
>>> plotting.scatter_matrix(data[['PIQ', 'VIQ', 'FSIQ']])
array([[<Axes: xlabel='PIQ', ylabel='PIQ'>,
        <Axes: xlabel='VIQ', ylabel='PIQ'>,
        <Axes: xlabel='FSIQ', ylabel='PIQ'>],
       [<Axes: xlabel='PIQ', ylabel='VIQ'>,
        <Axes: xlabel='VIQ', ylabel='VIQ'>,
        <Axes: xlabel='FSIQ', ylabel='VIQ'>],
       [<Axes: xlabel='PIQ', ylabel='FSIQ'>,
        <Axes: xlabel='VIQ', ylabel='FSIQ'>,
        <Axes: xlabel='FSIQ', ylabel='FSIQ'>]], dtype=object)

两个种群

IQ 指标呈双峰分布，仿佛存在两个亚群体。

练习

绘制仅男性和仅女性的散点矩阵。您认为这两个亚群体对应于性别吗？

3.1.2. 假设检验：比较两个组

对于简单的 统计检验，我们将使用 scipy.stats 的 SciPy 子模块。

>>> import scipy as sp

另请参阅

SciPy 是一个庞大的库。有关整个库的快速摘要，请参见 scipy 章节。

3.1.2.1. 学生 t 检验：最简单的统计检验

单样本检验：检验总体均值的值

scipy.stats.ttest_1samp() 检验原假设，即数据底层总体的均值等于给定值。它返回 T 统计量 和 p 值（请参见函数的帮助信息）。

>>> sp.stats.ttest_1samp(data['VIQ'], 0)
TtestResult(statistic=np.float64(30.088099970...), pvalue=np.float64(1.32891964...e-28), df=np.int64(39))

p 值为 表明，在原假设下不太可能观察到统计量的这种极端值。这可以被视为原假设为假，并且总体平均智商（VIQ 测量）不为 0 的证据。

从技术上讲，t 检验的 p 值是在假设从总体中抽取的样本的均值呈正态分布的情况下推导出来的。当总体本身呈正态分布时，此条件完全满足；但是，由于中心极限定理，对于从服从各种非正态分布的总体中抽取的相当大的样本，此条件几乎是正确的。

尽管如此，如果我们担心违反正态性假设会影响检验的结论，我们可以使用 Wilcoxon 符号秩检验，它以检验效力的代价放宽了这种假设。

>>> sp.stats.wilcoxon(data['VIQ'])
WilcoxonResult(statistic=np.float64(0.0), pvalue=np.float64(1.8189894...e-12))

双样本 t 检验：检验不同总体间的差异

我们已经看到，男性和女性样本中的平均 VIQ 不同。为了检验这种差异是否显著（并表明总体均值存在差异），我们使用 scipy.stats.ttest_ind() 执行双样本 t 检验。

>>> female_viq = data[data['Gender'] == 'Female']['VIQ']
>>> male_viq = data[data['Gender'] == 'Male']['VIQ']
>>> sp.stats.ttest_ind(female_viq, male_viq)
TtestResult(statistic=np.float64(-0.77261617232...), pvalue=np.float64(0.4445287677858...), df=np.float64(38.0))

相应的非参数检验是 Mann–Whitney U 检验，scipy.stats.mannwhitneyu()。

>>> sp.stats.mannwhitneyu(female_viq, male_viq)
MannwhitneyuResult(statistic=np.float64(164.5), pvalue=np.float64(0.34228868687...))

3.1.2.2. 配对检验：对同一组个体的重复测量

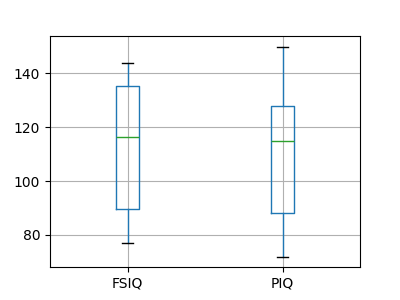
PIQ、VIQ 和 FSIQ 提供了三种智商测量指标。让我们检验 FISQ 和 PIQ 是否存在显著差异。我们可以使用“独立样本”检验。

>>> sp.stats.ttest_ind(data['FSIQ'], data['PIQ'])
TtestResult(statistic=np.float64(0.46563759638...), pvalue=np.float64(0.64277250...), df=np.float64(78.0))

这种方法的问题在于，它忽略了观测值之间的重要关系：FSIQ 和 PIQ 是对同一组个体进行测量的。因此，由于个体间变异性造成的方差是混杂的，降低了检验的效能。可以使用“配对检验”或 “重复测量检验” 来消除这种变异性。

>>> sp.stats.ttest_rel(data['FSIQ'], data['PIQ'])
TtestResult(statistic=np.float64(1.784201940...), pvalue=np.float64(0.082172638183...), df=np.int64(39))

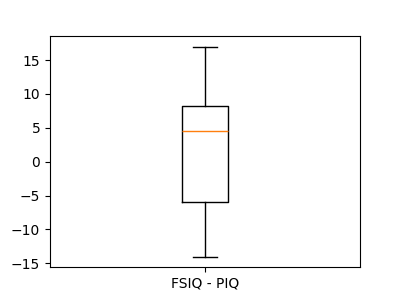
这等同于对配对观测值之间的差异进行单样本检验。

>>> sp.stats.ttest_1samp(data['FSIQ'] - data['PIQ'], 0)
TtestResult(statistic=np.float64(1.784201940...), pvalue=np.float64(0.082172638...), df=np.int64(39))

因此，我们可以使用 wilcoxon 执行检验的非参数版本。

>>> sp.stats.wilcoxon(data['FSIQ'], data['PIQ'], method="approx")
WilcoxonResult(statistic=np.float64(274.5), pvalue=np.float64(0.106594927135...))

练习

• 检验男性和女性体重之间的差异。

• 使用非参数统计检验男性和女性 VIQ 之间的差异。

结论：我们发现数据不支持男性和女性 VIQ 不同的假设。

3.1.3. 线性模型、多个因素和方差分析

3.1.3.1. 在 Python 中指定统计模型的“公式”

简单线性回归

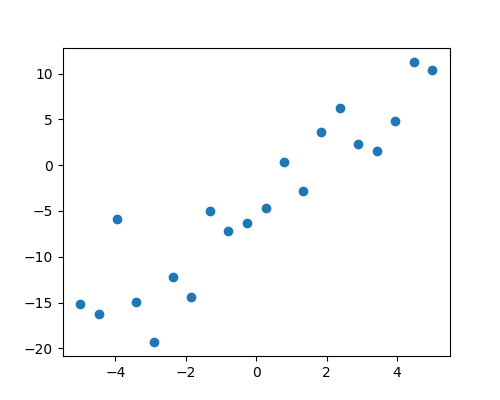
给定两组观测值，x 和 y，我们想要检验 y 是 x 的线性函数的假设。换句话说

其中 e 是观测噪声。我们将使用 statsmodels 模块来

1. 拟合线性模型。我们将使用最简单的策略，普通最小二乘法 (OLS)。

2. 检验 coef 是否非零。

首先，我们根据模型生成模拟数据

>>> import numpy as np
>>> x = np.linspace(-5, 5, 20)
>>> rng = np.random.default_rng(27446968)
>>> # normal distributed noise
>>> y = -5 + 3*x + 4 * rng.normal(size=x.shape)
>>> # Create a data frame containing all the relevant variables
>>> data = pandas.DataFrame({'x': x, 'y': y})

Python 中的统计“公式”

查看 statsmodels 文档

然后我们指定一个 OLS 模型并拟合它

>>> from statsmodels.formula.api import ols
>>> model = ols("y ~ x", data).fit()

我们可以检查从拟合中得出的各种统计信息

>>> print(model.summary()) 
                            OLS Regression Results
==============================================================================
Dep. Variable:                      y   R-squared:                       0.901
Model:                            OLS   Adj. R-squared:                  0.896
Method:                 Least Squares   F-statistic:                     164.5
Date:                             ...   Prob (F-statistic):           1.72e-10
Time:                             ...   Log-Likelihood:                -51.758
No. Observations:                  20   AIC:                             107.5
Df Residuals:                      18   BIC:                             109.5
Df Model:                           1
Covariance Type:            nonrobust
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
Intercept     -4.2948      0.759     -5.661      0.000      -5.889      -2.701
x              3.2060      0.250     12.825      0.000       2.681       3.731
==============================================================================
Omnibus:                        1.218   Durbin-Watson:                   1.796
Prob(Omnibus):                  0.544   Jarque-Bera (JB):                0.999
Skew:                           0.503   Prob(JB):                        0.607
Kurtosis:                       2.568   Cond. No.                         3.03
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

术语

Statsmodels 使用统计术语：statsmodels 中的 y 变量称为“内生变量”，而 x 变量称为外生变量。这里详细讨论了这一点 这里。

为了简化，y (内生) 是您要预测的值，而 x (外生) 代表您用来进行预测的特征。

练习

从上面的模型中检索估计参数。提示：使用制表符补全查找相关属性。

分类变量：比较组或多个类别

让我们回到大脑尺寸数据

>>> data = pandas.read_csv('examples/brain_size.csv', sep=';', na_values=".")

我们可以使用线性模型来编写男性和女性智商之间的比较

>>> model = ols("VIQ ~ Gender + 1", data).fit()
>>> print(model.summary()) 
                            OLS Regression Results
==============================================================================
Dep. Variable:                    VIQ   R-squared:                       0.015
Model:                            OLS   Adj. R-squared:                 -0.010
Method:                 Least Squares   F-statistic:                    0.5969
Date:                             ...   Prob (F-statistic):              0.445
Time:                             ...   Log-Likelihood:                -182.42
No. Observations:                  40   AIC:                             368.8
Df Residuals:                      38   BIC:                             372.2
Df Model:                           1
Covariance Type:            nonrobust
==================================================================================
                     coef    std err          t      P>|t|      [0.025      0.975]
----------------------------------------------------------------------------------
Intercept        109.4500      5.308     20.619      0.000      98.704     120.196
Gender[T.Male]     5.8000      7.507      0.773      0.445      -9.397      20.997
==============================================================================
Omnibus:                       26.188   Durbin-Watson:                   1.709
Prob(Omnibus):                  0.000   Jarque-Bera (JB):                3.703
Skew:                           0.010   Prob(JB):                        0.157
Kurtosis:                       1.510   Cond. No.                         2.62
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

指定模型的技巧

强制分类：“性别”自动检测为分类变量，因此其每个不同的值都被视为不同的实体。

可以使用以下方法将整型列强制转换为分类变量

>>> model = ols('VIQ ~ C(Gender)', data).fit()

截距：我们可以使用公式中的 - 1 删除截距，或者使用 + 1 强制使用截距。

小贴士

默认情况下，statsmodels 将具有 K 个可能值的分类变量视为 K-1 个“虚拟”布尔变量（最后一个级别被吸收到截距项中）。这几乎总是好的默认选择 - 但是，可以为分类变量指定不同的编码 (https://statsmodels.pythonlang.cn/devel/contrasts.html)。

链接到不同 FSIQ 和 PIQ 之间的 t 检验

要比较不同类型的智商，我们需要创建一个“长格式”表格，列出智商，其中智商的类型由分类变量表示

>>> data_fisq = pandas.DataFrame({'iq': data['FSIQ'], 'type': 'fsiq'})
>>> data_piq = pandas.DataFrame({'iq': data['PIQ'], 'type': 'piq'})
>>> data_long = pandas.concat((data_fisq, data_piq))
>>> print(data_long)
     iq  type
0   133  fsiq
1   140  fsiq
2   139  fsiq
3   133  fsiq
4   137  fsiq
...  ...   ...
35  128   piq
36  124   piq
37   94   piq
38   74   piq
39   89   piq

[80 rows x 2 columns]

>>> model = ols("iq ~ type", data_long).fit()
>>> print(model.summary()) 
                            OLS Regression Results
...
==========================...
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------...
Intercept     113.4500      3.683     30.807      0.000       106.119   120.781
type[T.piq]    -2.4250      5.208     -0.466      0.643       -12.793     7.943
...

我们可以看到，我们为不同类型智商的影响获得了与之前的 t 检验相同的 t 检验值和相应的 p 值。

>>> sp.stats.ttest_ind(data['FSIQ'], data['PIQ'])
TtestResult(statistic=np.float64(0.46563759638...), pvalue=np.float64(0.64277250...), df=np.float64(78.0))

3.1.3.2. 多元回归：包含多个因素

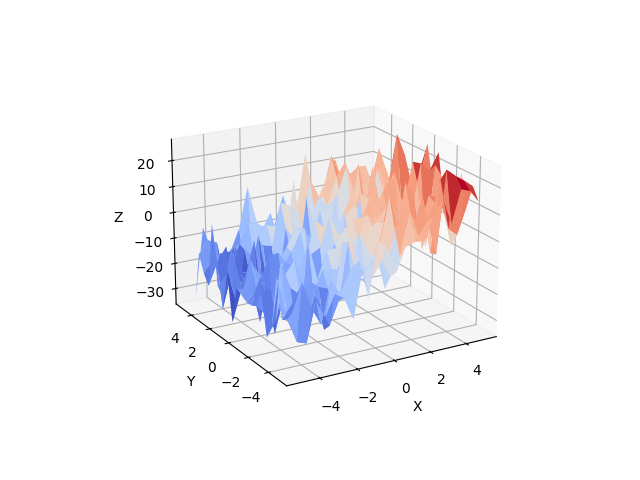
考虑一个线性模型，该模型用 2 个变量 x 和 y 来解释一个变量 z（因变量）。

这样的模型可以在 3D 中被视为将一个平面拟合到 (x，y，z) 点的云中。

示例：鸢尾花数据 (examples/iris.csv)

小贴士

萼片和花瓣的大小往往是相关的：更大的花朵更大！但是，除了物种之外，是否还存在系统性影响？

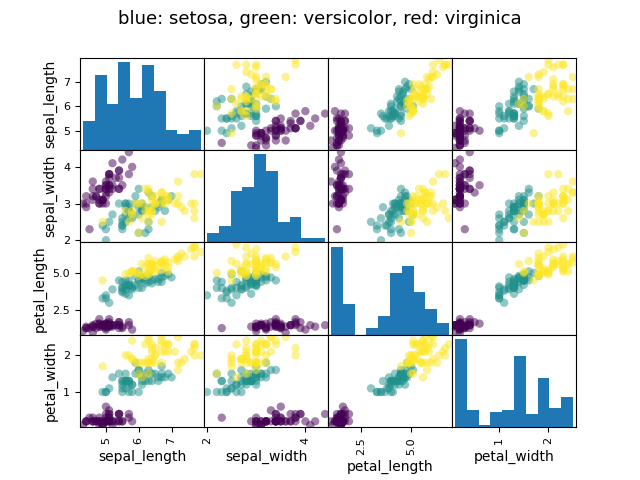
>>> data = pandas.read_csv('examples/iris.csv')
>>> model = ols('sepal_width ~ name + petal_length', data).fit()
>>> print(model.summary()) 
                            OLS Regression Results
==========================...
Dep. Variable:            sepal_width   R-squared:                       0.478
Model:                            OLS   Adj. R-squared:                  0.468
Method:                 Least Squares   F-statistic:                     44.63
Date:                             ...   Prob (F-statistic):           1.58e-20
Time:                             ...   Log-Likelihood:                -38.185
No. Observations:                 150   AIC:                             84.37
Df Residuals:                     146   BIC:                             96.41
Df Model:                           3
Covariance Type:            nonrobust
==========================...
                         coef    std err          t     P>|t|  [0.025      0.975]
------------------------------------------...
Intercept              2.9813      0.099     29.989     0.000      2.785     3.178
name[T.versicolor]    -1.4821      0.181     -8.190     0.000     -1.840    -1.124
name[T.virginica]     -1.6635      0.256     -6.502     0.000     -2.169    -1.158
petal_length           0.2983      0.061      4.920     0.000      0.178     0.418
==========================...
Omnibus:                        2.868   Durbin-Watson:                   1.753
Prob(Omnibus):                  0.238   Jarque-Bera (JB):                2.885
Skew:                          -0.082   Prob(JB):                        0.236
Kurtosis:                       3.659   Cond. No.                         54.0
==========================...

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

3.1.3.3. 事后假设检验：方差分析 (ANOVA)

在上面的鸢尾花示例中，我们希望检验在去除萼片宽度影响后，花瓣长度在变色鸢尾和维吉尼亚鸢尾之间是否存在差异。这可以表述为检验上面估计的线性模型中与变色鸢尾和维吉尼亚鸢尾相关的系数之间的差异（它是一个方差分析，ANOVA）。为此，我们在估计的参数上写一个“对比”向量：我们想要检验 "name[T.versicolor] - name[T.virginica]"，使用 F 检验

>>> print(model.f_test([0, 1, -1, 0]))
<F test: F=3.24533535..., p=0.07369..., df_denom=146, df_num=1>

这种差异是否显著？

练习

回到大脑尺寸 + 智商数据，检验在去除大脑尺寸、身高和体重影响后，男性和女性的 VIQ 是否存在差异。

3.1.4. 更多可视化：用于统计探索的 seaborn

Seaborn 将简单的统计拟合与 pandas 数据框上的绘图相结合。

让我们考虑一个数据，该数据提供了 500 个人的工资和其他许多个人信息 (Berndt, ER. The Practice of Econometrics. 1991. NY: Addison-Wesley)。

小贴士

加载和绘制工资数据的完整代码位于 相应的示例 中。

>>> print(data)  
     EDUCATION  SOUTH  SEX  EXPERIENCE  UNION      WAGE  AGE  RACE  \
0            8      0    1          21      0  0.707570   35     2
1            9      0    1          42      0  0.694605   57     3
2           12      0    0           1      0  0.824126   19     3
3           12      0    0           4      0  0.602060   22     3
...

3.1.4.1. Pairplot：散点矩阵

我们可以使用 seaborn.pairplot() 来轻松直观地了解连续变量之间的交互作用，以显示散点矩阵

>>> import seaborn
>>> seaborn.pairplot(data, vars=['WAGE', 'AGE', 'EDUCATION'],
...                  kind='reg')  

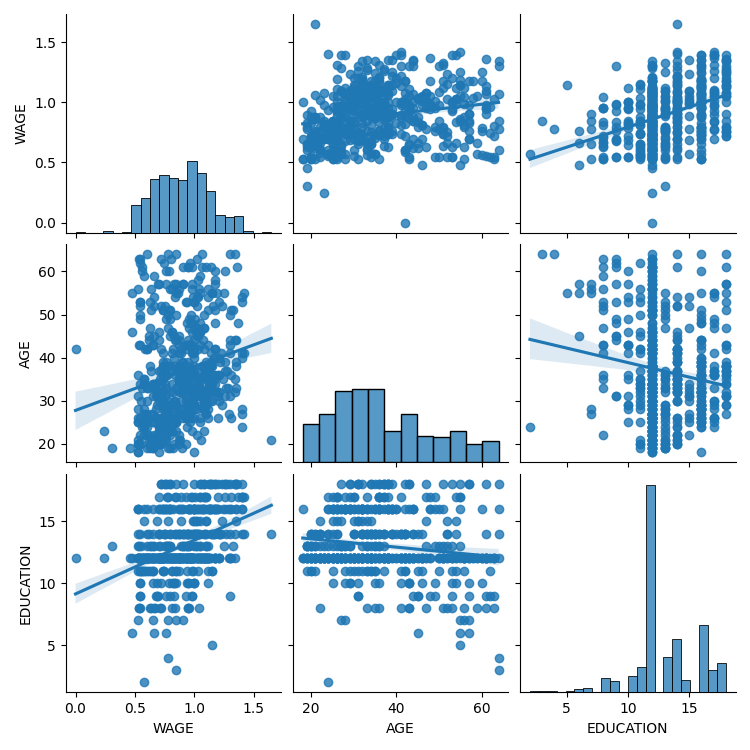
分类变量可以作为色调绘制

>>> seaborn.pairplot(data, vars=['WAGE', 'AGE', 'EDUCATION'],
...                  kind='reg', hue='SEX')  

外观和感觉以及 matplotlib 设置

Seaborn 更改 matplotlib 图形的默认设置，以实现更“现代”、更“类似 Excel”的外观。它在导入时执行此操作。您可以使用以下命令重置默认值

>>> import matplotlib.pyplot as plt
>>> plt.rcdefaults()

小贴士

要切换回 seaborn 设置，或更好地了解 seaborn 中的样式，请参阅 seaborn 文档的相关部分。

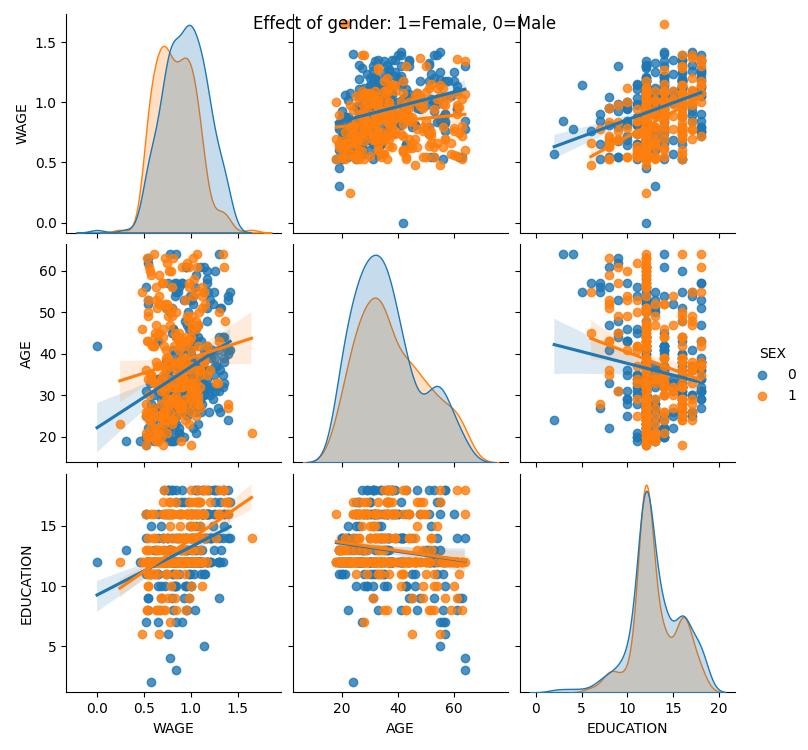
3.1.4.2. lmplot：绘制单变量回归

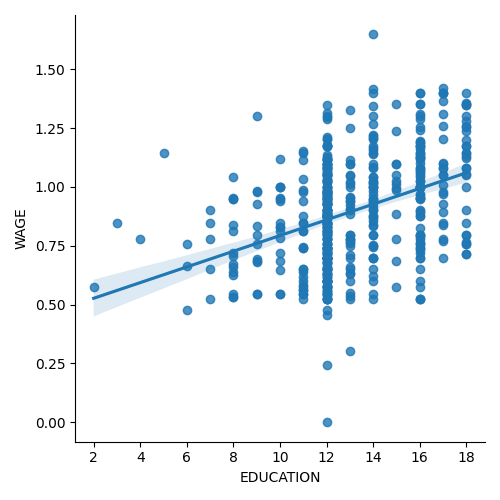
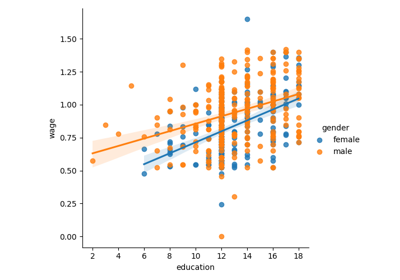
可以利用 seaborn.lmplot() 绘制一个回归，该回归捕获了一个变量与另一个变量之间的关系，例如工资和教育。

>>> seaborn.lmplot(y='WAGE', x='EDUCATION', data=data)  

稳健回归

小贴士

鉴于在上面的图中，似乎有几个数据点位于右侧的主要云之外，它们可能是异常值，不能代表总体，但会驱动回归。

要计算对异常值不太敏感的回归，必须使用 稳健模型。这在 seaborn 中是通过在绘图函数中使用 robust=True 完成的，或者在 statsmodels 中通过用“稳健线性模型”替换 OLS 的使用来完成，statsmodels.formula.api.rlm()。

3.1.5. 检验交互作用

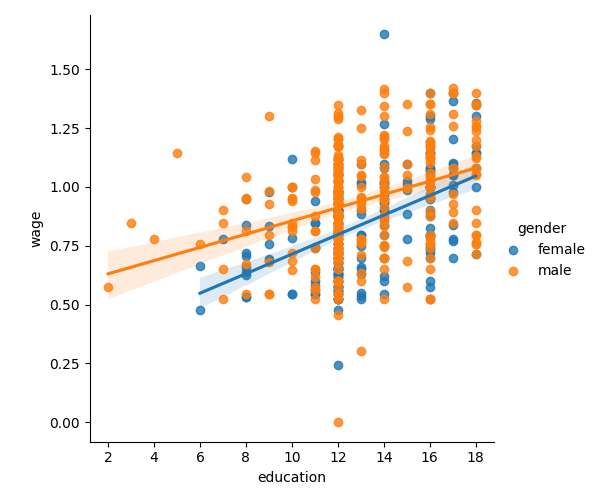
男性的工资随着教育水平的提高而增加的幅度是否比女性更大？

小贴士

上面的图是由两个不同的拟合组成的。我们需要制定一个单一模型来检验两个总体之间斜率的变化。这是通过 “交互作用” 完成的。

>>> result = sm.ols(formula='wage ~ education + gender + education * gender',
...                 data=data).fit()    
>>> print(result.summary())    
...
                            coef    std err    t     P>|t|  [0.025      0.975]
------------------------------------------------------------------------------
Intercept                   0.2998   0.072    4.173   0.000     0.159   0.441
gender[T.male]              0.2750   0.093    2.972   0.003     0.093   0.457
education                   0.0415   0.005    7.647   0.000     0.031   0.052
education:gender[T.male]   -0.0134   0.007   -1.919   0.056    -0.027   0.000
==========================...
...

我们能否得出结论，教育对男性的益处大于女性？

要点

• 假设检验和 p 值可以告诉您影响/差异的显著性。

• 公式（使用分类变量）使您能够在数据中表达丰富的联系。

• 可视化您的数据并拟合简单的模型可以洞察数据。

• 条件化（添加可以解释所有或部分变异的因素）是重要的建模方面，它会改变解释。

3.1.6. 图形的完整代码

统计章节的代码示例。

箱线图和配对差异

箱线图和配对差异

绘制 pandas 数据框的简单数量

绘制 pandas 数据框的简单数量

分析鸢尾花花瓣和萼片的大小

分析鸢尾花花瓣和萼片的大小

简单回归

简单回归

多元回归

多元回归

检验工资中教育/性别的交互作用

检验工资中教育/性别的交互作用

可视化影响工资的因素

可视化影响工资的因素

9/11 事件之前和之后的机票价格

9/11 事件之前和之后的机票价格

3.1.7. 本章练习的解答

将性别和智商联系起来

将性别和智商联系起来