3.1.6.8. 9/11 前后的机票价格

这是一个类似商业智能 (BI) 的应用程序。

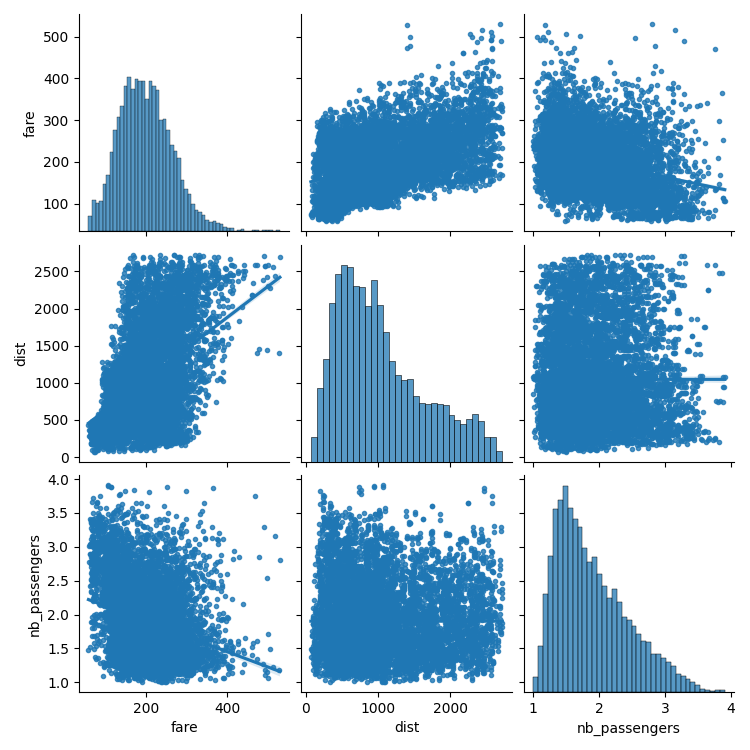
有趣的是，我们可能希望研究机票价格随年份的变化，并根据行程进行配对，或者忽略年份，只作为行程终点的函数。

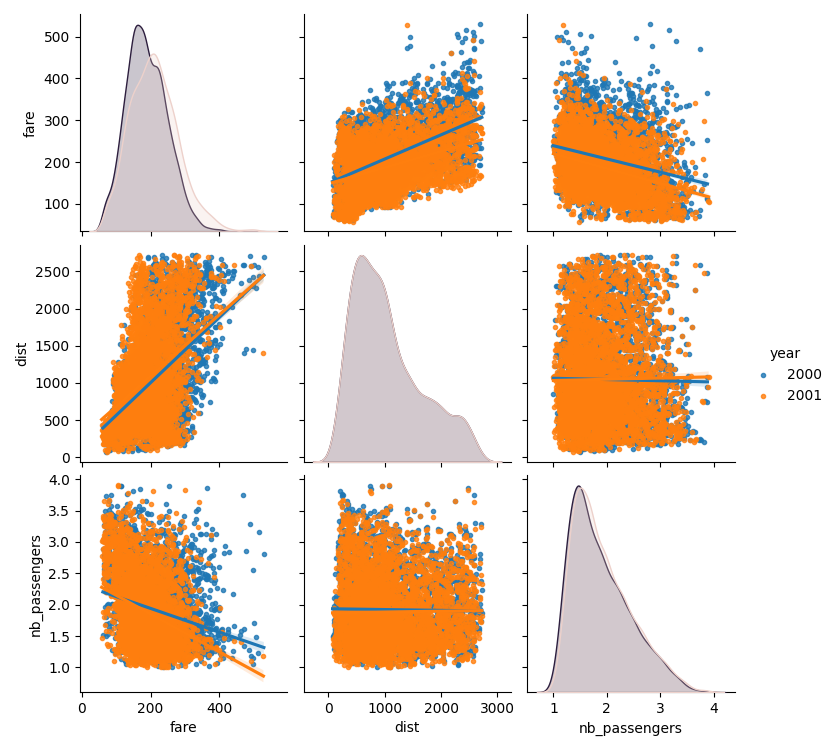
使用 statsmodels 的线性模型，我们发现，无论是使用 OLS（普通最小二乘）还是稳健拟合，截距和斜率都显著不为零：机票价格在 2000 年至 2001 年间下降，并且它们对行程距离的依赖性也下降了

# Standard library imports
import os

加载数据

import pandas
import requests

if not os.path.exists("airfares.txt"):
    # Download the file if it is not present
    r = requests.get(
        "https://users.stat.ufl.edu/~winner/data/airq4.dat",
        verify=False,  # Wouldn't normally do this, but this site's certificate
        # is not yet distributed
    )
    with open("airfares.txt", "wb") as f:
        f.write(r.content)

# As a separator, ' +' is a regular expression that means 'one of more
# space'
data = pandas.read_csv(
    "airfares.txt",
    delim_whitespace=True,
    header=0,
    names=[
        "city1",
        "city2",
        "pop1",
        "pop2",
        "dist",
        "fare_2000",
        "nb_passengers_2000",
        "fare_2001",
        "nb_passengers_2001",
    ],
)

# we log-transform the number of passengers
import numpy as np

data["nb_passengers_2000"] = np.log10(data["nb_passengers_2000"])
data["nb_passengers_2001"] = np.log10(data["nb_passengers_2001"])

/home/runner/work/scientific-python-lectures/scientific-python-lectures/packages/statistics/examples/plot_airfare.py:38: FutureWarning: The 'delim_whitespace' keyword in pd.read_csv is deprecated and will be removed in a future version. Use ``sep='\s+'`` instead
  data = pandas.read_csv(

创建一个以年份为属性的数据帧，而不是单独的列

# This involves a small danse in which we separate the dataframes in 2,
# one for year 2000, and one for 2001, before concatenating again.

# Make an index of each flight
data_flat = data.reset_index()

data_2000 = data_flat[
    ["city1", "city2", "pop1", "pop2", "dist", "fare_2000", "nb_passengers_2000"]
]
# Rename the columns
data_2000.columns = pandas.Index(
    ["city1", "city2", "pop1", "pop2", "dist", "fare", "nb_passengers"]
)
# Add a column with the year
data_2000.insert(0, "year", 2000)

data_2001 = data_flat[
    ["city1", "city2", "pop1", "pop2", "dist", "fare_2001", "nb_passengers_2001"]
]
# Rename the columns
data_2001.columns = pandas.Index(
    ["city1", "city2", "pop1", "pop2", "dist", "fare", "nb_passengers"]
)
# Add a column with the year
data_2001.insert(0, "year", 2001)

data_flat = pandas.concat([data_2000, data_2001])

绘制散点矩阵，突出显示不同的方面

import seaborn

seaborn.pairplot(
    data_flat, vars=["fare", "dist", "nb_passengers"], kind="reg", markers="."
)

# A second plot, to show the effect of the year (ie the 9/11 effect)
seaborn.pairplot(
    data_flat,
    vars=["fare", "dist", "nb_passengers"],
    kind="reg",
    hue="year",
    markers=".",
)

• 
• 

<seaborn.axisgrid.PairGrid object at 0x7f78e5312f30>

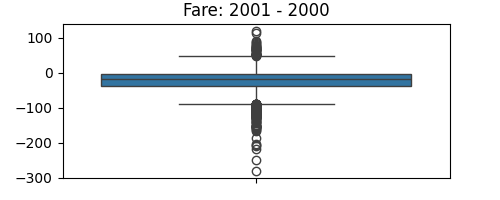
绘制机票价格差异

import matplotlib.pyplot as plt

plt.figure(figsize=(5, 2))
seaborn.boxplot(data.fare_2001 - data.fare_2000)
plt.title("Fare: 2001 - 2000")
plt.subplots_adjust()

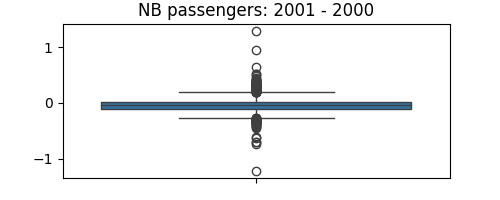
plt.figure(figsize=(5, 2))
seaborn.boxplot(data.nb_passengers_2001 - data.nb_passengers_2000)
plt.title("NB passengers: 2001 - 2000")
plt.subplots_adjust()

• 
• 

统计检验：机票价格对距离和乘客数量的依赖性

import statsmodels.formula.api as sm

result = sm.ols(formula="fare ~ 1 + dist + nb_passengers", data=data_flat).fit()
print(result.summary())

# Using a robust fit
result = sm.rlm(formula="fare ~ 1 + dist + nb_passengers", data=data_flat).fit()
print(result.summary())

                            OLS Regression Results
==============================================================================
Dep. Variable:                   fare   R-squared:                       0.275
Model:                            OLS   Adj. R-squared:                  0.275
Method:                 Least Squares   F-statistic:                     1585.
Date:                Mon, 07 Oct 2024   Prob (F-statistic):               0.00
Time:                        04:57:10   Log-Likelihood:                -45532.
No. Observations:                8352   AIC:                         9.107e+04
Df Residuals:                    8349   BIC:                         9.109e+04
Df Model:                           2
Covariance Type:            nonrobust
=================================================================================
                    coef    std err          t      P>|t|      [0.025      0.975]
---------------------------------------------------------------------------------
Intercept       211.2428      2.466     85.669      0.000     206.409     216.076
dist              0.0484      0.001     48.149      0.000       0.046       0.050
nb_passengers   -32.8925      1.127    -29.191      0.000     -35.101     -30.684
==============================================================================
Omnibus:                      604.051   Durbin-Watson:                   1.446
Prob(Omnibus):                  0.000   Jarque-Bera (JB):              740.733
Skew:                           0.710   Prob(JB):                    1.42e-161
Kurtosis:                       3.338   Cond. No.                     5.23e+03
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 5.23e+03. This might indicate that there are
strong multicollinearity or other numerical problems.
                    Robust linear Model Regression Results
==============================================================================
Dep. Variable:                   fare   No. Observations:                 8352
Model:                            RLM   Df Residuals:                     8349
Method:                          IRLS   Df Model:                            2
Norm:                          HuberT
Scale Est.:                       mad
Cov Type:                          H1
Date:                Mon, 07 Oct 2024
Time:                        04:57:10
No. Iterations:                    12
=================================================================================
                    coef    std err          z      P>|z|      [0.025      0.975]
---------------------------------------------------------------------------------
Intercept       215.0848      2.448     87.856      0.000     210.287     219.883
dist              0.0460      0.001     46.166      0.000       0.044       0.048
nb_passengers   -35.2686      1.119    -31.526      0.000     -37.461     -33.076
=================================================================================

If the model instance has been used for another fit with different fit parameters, then the fit options might not be the correct ones anymore .

统计检验：机票价格对距离的回归：2001/2000 的差异

result = sm.ols(formula="fare_2001 - fare_2000 ~ 1 + dist", data=data).fit()
print(result.summary())

# Plot the corresponding regression
data["fare_difference"] = data["fare_2001"] - data["fare_2000"]
seaborn.lmplot(x="dist", y="fare_difference", data=data)

plt.show()

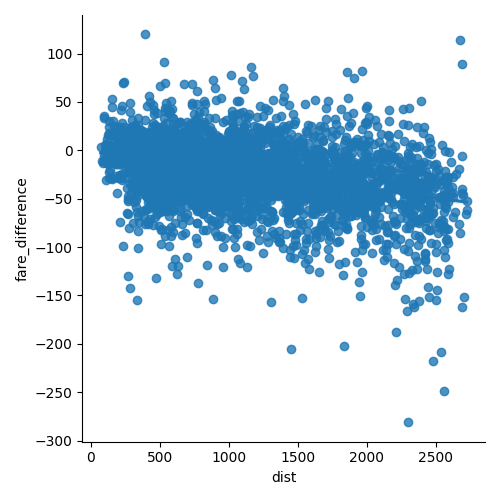
                            OLS Regression Results
==============================================================================
Dep. Variable:              fare_2001   R-squared:                       0.159
Model:                            OLS   Adj. R-squared:                  0.159
Method:                 Least Squares   F-statistic:                     791.7
Date:                Mon, 07 Oct 2024   Prob (F-statistic):          1.20e-159
Time:                        04:57:10   Log-Likelihood:                -22640.
No. Observations:                4176   AIC:                         4.528e+04
Df Residuals:                    4174   BIC:                         4.530e+04
Df Model:                           1
Covariance Type:            nonrobust
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
Intercept    148.0279      1.673     88.480      0.000     144.748     151.308
dist           0.0388      0.001     28.136      0.000       0.036       0.041
==============================================================================
Omnibus:                      136.558   Durbin-Watson:                   1.544
Prob(Omnibus):                  0.000   Jarque-Bera (JB):              149.624
Skew:                           0.462   Prob(JB):                     3.23e-33
Kurtosis:                       2.920   Cond. No.                     2.40e+03
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 2.4e+03. This might indicate that there are
strong multicollinearity or other numerical problems.