3.4.8.7. 线性模型中的方差和正则化可视化

import numpy as np

# Smaller figures
import matplotlib.pyplot as plt

plt.rcParams["figure.figsize"] = (3, 2)

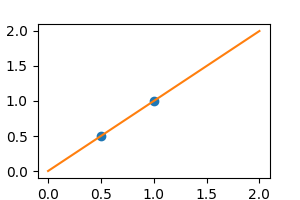
我们考虑只有2个数据点的情况

X = np.c_[0.5, 1].T
y = [0.5, 1]
X_test = np.c_[0, 2].T

在没有噪声的情况下，线性回归完美拟合数据

from sklearn import linear_model

regr = linear_model.LinearRegression()
regr.fit(X, y)
plt.plot(X, y, "o")
plt.plot(X_test, regr.predict(X_test))

[<matplotlib.lines.Line2D object at 0x7f78e6f06510>]

在现实生活中，我们的数据中存在噪声（例如测量噪声）

rng = np.random.default_rng(27446968)
for _ in range(6):
    noisy_X = X + np.random.normal(loc=0, scale=0.1, size=X.shape)
    plt.plot(noisy_X, y, "o")
    regr.fit(noisy_X, y)
    plt.plot(X_test, regr.predict(X_test))

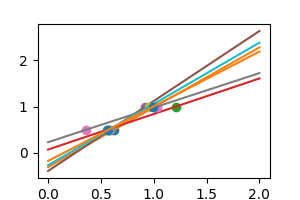
我们可以看到，我们的线性模型捕获并放大了数据中的噪声。它显示出很大的方差。

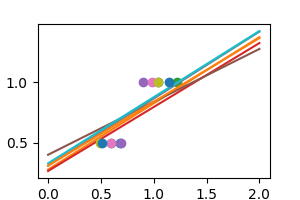
我们可以使用另一个使用正则化的线性估计器，即 Ridge 估计器。该估计器通过将系数缩小到零来正则化它们，假设非常高的相关性通常是虚假的。alpha 参数控制使用的收缩量。

regr = linear_model.Ridge(alpha=0.1)
np.random.seed(0)
for _ in range(6):
    noisy_X = X + np.random.normal(loc=0, scale=0.1, size=X.shape)
    plt.plot(noisy_X, y, "o")
    regr.fit(noisy_X, y)
    plt.plot(X_test, regr.predict(X_test))

plt.show()