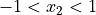2.7. 数学优化:寻找函数的最小值¶
作者:Gaël Varoquaux
数学优化 处理的是数值上寻找函数的最小值(或最大值或零点)的问题。在这种情况下,函数被称为代价函数、目标函数或能量。
在这里,我们感兴趣的是使用 scipy.optimize 进行黑盒优化:我们不依赖于我们正在优化的函数的数学表达式。请注意,此表达式通常可用于更有效、非黑盒的优化。
另请参阅
参考文献
数学优化非常……数学化。如果您想要性能,阅读书籍确实会有回报
2.7.1. 了解你的问题¶
并非所有优化问题都相同。了解你的问题可以让你选择合适的工具。
2.7.1.1. 凸优化与非凸优化¶
|
|
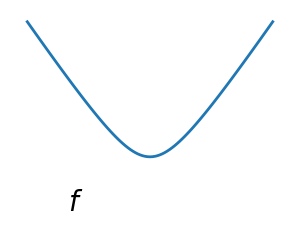
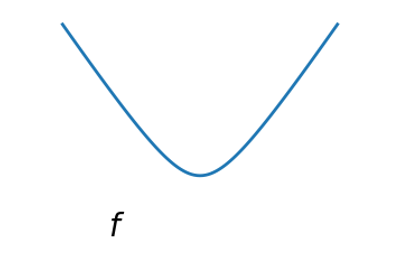
凸函数:
|
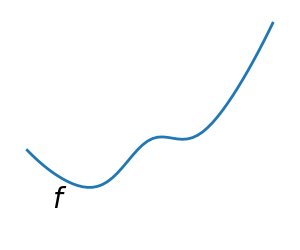
非凸函数 |
优化凸函数很容易。优化非凸函数可能非常困难。
注意
可以证明,对于凸函数,局部最小值也是全局最小值。然后,在某种意义上,最小值是唯一的。
2.7.1.2. 光滑问题与非光滑问题¶
|
|
光滑函数: 梯度在任何地方都定义,并且是连续函数 |
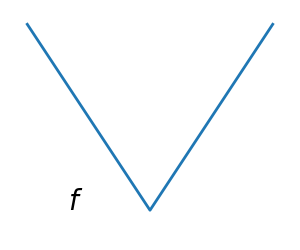
非光滑函数 |
优化光滑函数更容易(在黑盒优化的上下文中为真,否则线性规划 是处理分段线性函数非常有效的示例)。
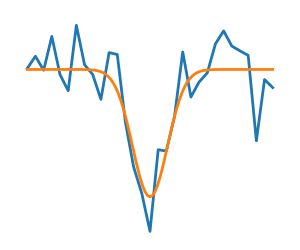
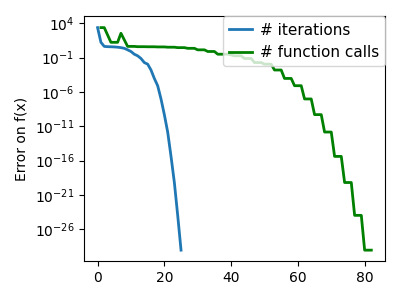
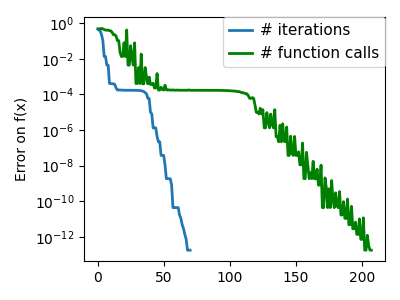
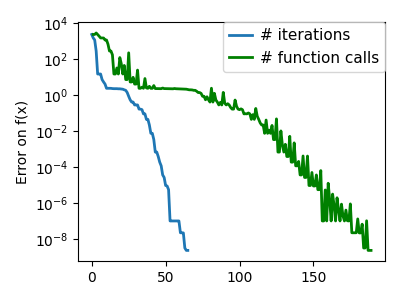
2.7.1.3. 有噪声与无噪声代价函数¶
有噪声(蓝色)和无噪声(绿色)函数 |
|
2.7.1.4. 约束¶
带约束的优化 这里
|
2.7.2. 不同优化器的回顾¶
2.7.2.1. 入门:一维优化¶
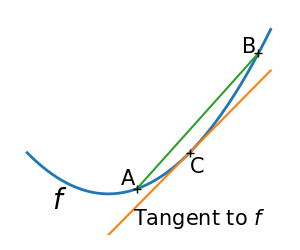
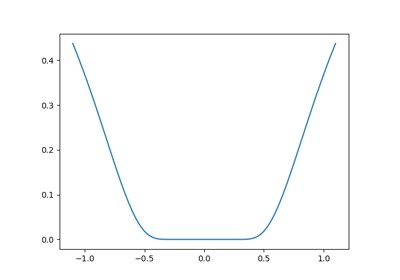
让我们从寻找标量函数 ![f(x)=\exp[(x-0.5)^2]](../../_images/math/2edc5eeddc22a27d97b43dd58e8effdc3cdbb50e.png) 的最小值开始。
的最小值开始。 scipy.optimize.minimize_scalar() 使用 Brent 方法查找函数的最小值
>>> import numpy as np
>>> import scipy as sp
>>> def f(x):
... return -np.exp(-(x - 0.5)**2)
>>> result = sp.optimize.minimize_scalar(f)
>>> result.success # check if solver was successful
True
>>> x_min = result.x
>>> x_min
np.float64(0.50...)
>>> x_min - 0.5
np.float64(5.8...e-09)
注意
您可以使用不同的求解器,使用参数 method。
注意
scipy.optimize.minimize_scalar() 还可以用于使用参数 bounds 约束到区间的优化。
2.7.2.2. 基于梯度的方法¶
关于梯度下降的一些直觉¶
这里我们关注的是直觉,而不是代码。代码将在后面介绍。
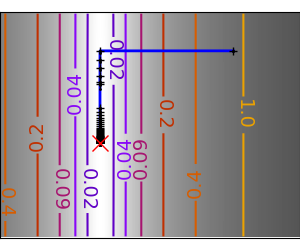
梯度下降 基本上包括沿着梯度的方向(即最速下降的方向)采取小步。
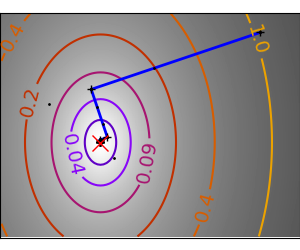
一个条件良好的二次函数。 |
||
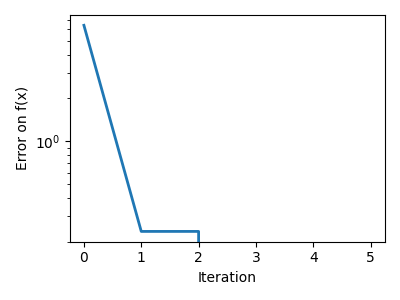
一个条件不好的二次函数。 梯度方法在条件不好的问题上的核心问题是梯度往往不指向最小值的方向。 |
我们可以看到,非常各向异性(条件不好)的函数更难优化。
此外,采取更大的步长显然是有利的。这在梯度下降代码中使用线搜索来完成。
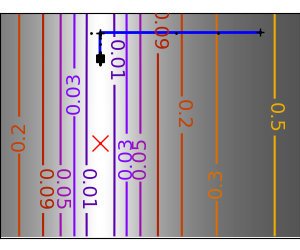
一个条件良好的二次函数。 |
||
一个条件不好的二次函数。 |
||
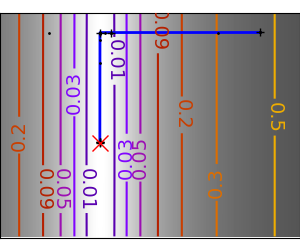
一个条件不好的非二次函数。 |
||
一个条件非常不好的非二次函数。 |
函数越像二次函数(椭圆等值线),优化就越容易。
共轭梯度下降¶
上述梯度下降算法是玩具,不应在实际问题中使用。
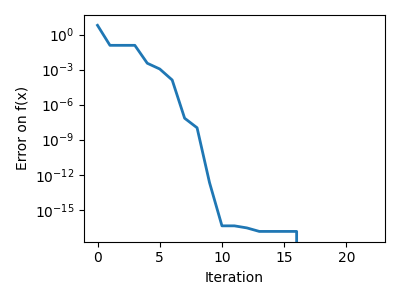
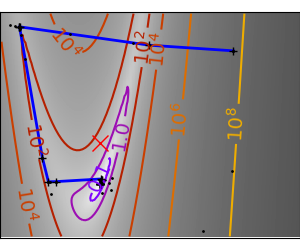
从上面的实验可以看出,简单梯度下降算法的问题之一是它往往会在山谷中振荡,每次都遵循梯度的方向,这使得它穿过山谷。共轭梯度通过添加一个摩擦项来解决此问题:每个步骤都依赖于梯度的最后两个值,并且锐角转弯减少了。
一个条件不好的非二次函数。 |
||
一个条件非常不好的非二次函数。 |
SciPy 提供 scipy.optimize.minimize() 来查找一个或多个变量的标量函数的最小值。通过将参数 method 设置为 CG,可以使用简单的共轭梯度方法
>>> def f(x): # The rosenbrock function
... return .5*(1 - x[0])**2 + (x[1] - x[0]**2)**2
>>> sp.optimize.minimize(f, [2, -1], method="CG")
message: Optimization terminated successfully.
success: True
status: 0
fun: 1.650...e-11
x: [ 1.000e+00 1.000e+00]
nit: 13
jac: [-6.15...e-06 2.53...e-07]
nfev: 81
njev: 27
梯度方法需要函数的雅可比矩阵(梯度)。它们可以数值计算它,但如果您能传递给它们梯度,则会执行得更好
>>> def jacobian(x):
... return np.array((-2*.5*(1 - x[0]) - 4*x[0]*(x[1] - x[0]**2), 2*(x[1] - x[0]**2)))
>>> sp.optimize.minimize(f, [2, 1], method="CG", jac=jacobian)
message: Optimization terminated successfully.
success: True
status: 0
fun: 2.95786...e-14
x: [ 1.000e+00 1.000e+00]
nit: 8
jac: [ 7.183e-07 -2.990e-07]
nfev: 16
njev: 16
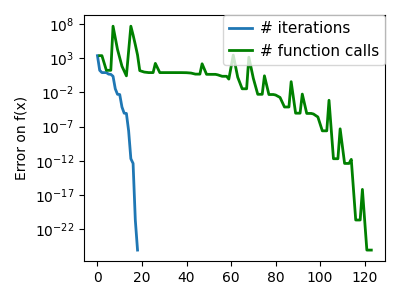
请注意,函数仅评估了 27 次,而没有梯度则为 108 次。
2.7.2.3. 牛顿法和拟牛顿法¶
牛顿法:使用 Hessian 矩阵(二阶导数)¶
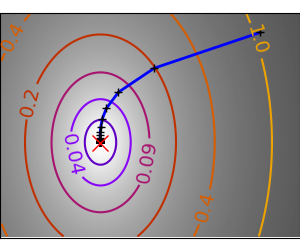
牛顿法 使用局部二次近似来计算跳跃方向。为此,它们依赖于函数的 2 个一阶导数:梯度和Hessian 矩阵。
一个条件不好的二次函数 请注意,由于二次近似是精确的,因此牛顿法非常快 |
||
一个条件不好的非二次函数 这里我们正在优化一个高斯函数,它始终在其二次近似之下。因此,牛顿法过度补偿并导致振荡。 |
||
一个条件非常不好的非二次函数 |
在 SciPy 中,您可以通过将 method 设置为 Newton-CG 来使用牛顿方法 scipy.optimize.minimize()。这里,CG 指的是通过共轭梯度进行 Hessian 矩阵的内部求逆。
>>> def f(x): # The rosenbrock function
... return .5*(1 - x[0])**2 + (x[1] - x[0]**2)**2
>>> def jacobian(x):
... return np.array((-2*.5*(1 - x[0]) - 4*x[0]*(x[1] - x[0]**2), 2*(x[1] - x[0]**2)))
>>> sp.optimize.minimize(f, [2,-1], method="Newton-CG", jac=jacobian)
message: Optimization terminated successfully.
success: True
status: 0
fun: 1.5601357400786612e-15
x: [ 1.000e+00 1.000e+00]
nit: 10
jac: [ 1.058e-07 -7.483e-08]
nfev: 11
njev: 33
nhev: 0
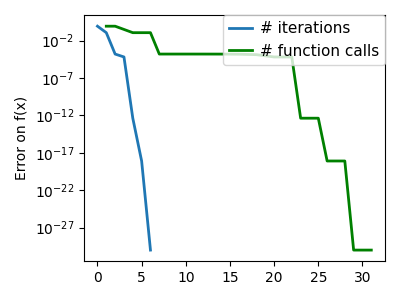
请注意,与共轭梯度法(上面)相比,牛顿法需要较少的函数评估次数,但需要更多的梯度评估次数,因为它使用梯度来近似 Hessian 矩阵。让我们计算 Hessian 矩阵并将其传递给算法。
>>> def hessian(x): # Computed with sympy
... return np.array(((1 - 4*x[1] + 12*x[0]**2, -4*x[0]), (-4*x[0], 2)))
>>> sp.optimize.minimize(f, [2,-1], method="Newton-CG", jac=jacobian, hess=hessian)
message: Optimization terminated successfully.
success: True
status: 0
fun: 1.6277298383706738e-15
x: [ 1.000e+00 1.000e+00]
nit: 10
jac: [ 1.110e-07 -7.781e-08]
nfev: 11
njev: 11
nhev: 10
注意
在非常高维的情况下,Hessian 矩阵的求逆可能代价高昂且不稳定(大规模 > 250)。
注意
牛顿优化器不应与基于相同原理的牛顿求根方法混淆,scipy.optimize.newton()。
拟牛顿方法:动态近似 Hessian 矩阵¶
BFGS:BFGS(Broyden-Fletcher-Goldfarb-Shanno 算法)在每一步都细化 Hessian 矩阵的近似值。
2.7.3. 完整代码示例¶
2.7.4. 数学优化章节示例¶
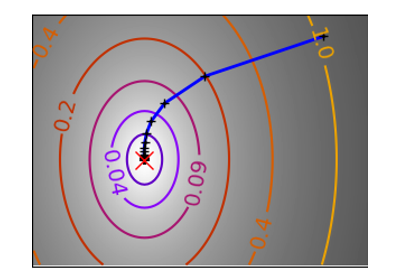
一个条件不好的二次函数 在完全二次函数上,BFGS 的速度不如牛顿法,但仍然非常快。 |
||
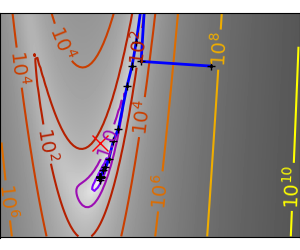
一个条件不好的非二次函数 在这里,BFGS 比牛顿法表现更好,因为其对曲率的经验估计优于 Hessian 矩阵提供的估计。 |
||
一个条件非常不好的非二次函数 |
>>> def f(x): # The rosenbrock function
... return .5*(1 - x[0])**2 + (x[1] - x[0]**2)**2
>>> def jacobian(x):
... return np.array((-2*.5*(1 - x[0]) - 4*x[0]*(x[1] - x[0]**2), 2*(x[1] - x[0]**2)))
>>> sp.optimize.minimize(f, [2, -1], method="BFGS", jac=jacobian)
message: Optimization terminated successfully.
success: True
status: 0
fun: 2.630637192365927e-16
x: [ 1.000e+00 1.000e+00]
nit: 8
jac: [ 6.709e-08 -3.222e-08]
hess_inv: [[ 9.999e-01 2.000e+00]
[ 2.000e+00 4.499e+00]]
nfev: 10
njev: 10
L-BFGS:有限内存 BFGS 介于 BFGS 和共轭梯度之间:在非常高维(> 250)的情况下,Hessian 矩阵的计算和求逆成本过高。L-BFGS 保留了一个低秩版本。此外,L-BFGS-B 也支持边界约束。
>>> def f(x): # The rosenbrock function
... return .5*(1 - x[0])**2 + (x[1] - x[0]**2)**2
>>> def jacobian(x):
... return np.array((-2*.5*(1 - x[0]) - 4*x[0]*(x[1] - x[0]**2), 2*(x[1] - x[0]**2)))
>>> sp.optimize.minimize(f, [2, 2], method="L-BFGS-B", jac=jacobian)
message: CONVERGENCE: NORM_OF_PROJECTED_GRADIENT_<=_PGTOL
success: True
status: 0
fun: 1.4417677473...e-15
x: [ 1.000e+00 1.000e+00]
nit: 16
jac: [ 1.023e-07 -2.593e-08]
nfev: 17
njev: 17
hess_inv: <2x2 LbfgsInvHessProduct with dtype=float64>
2.7.4.12. 无梯度方法¶
一种射击方法:Powell 算法¶
几乎是一种梯度方法
一个条件不好的二次函数 Powell 方法对低维空间中的局部病态条件不太敏感。 |
||
一个条件非常不好的非二次函数 |
单纯形方法:Nelder-Mead¶
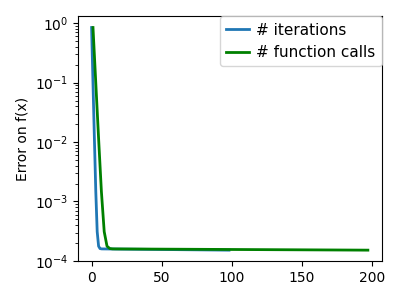
Nelder-Mead 算法是将二分法推广到高维空间。该算法通过细化一个 单纯形(区间和三角形到高维空间的推广)来限定最小值。
优点:它对噪声具有鲁棒性,因为它不依赖于计算梯度。因此,只要它们显示出大规模的钟形行为,它就可以处理非局部平滑的函数,例如实验数据点。但是,在平滑的、无噪声的函数上,它比基于梯度的方法慢。
一个条件不好的非二次函数 |
||
一个条件非常不好的非二次函数 |
在 scipy.optimize.minimize() 中使用 Nelder-Mead 求解器。
>>> def f(x): # The rosenbrock function
... return .5*(1 - x[0])**2 + (x[1] - x[0]**2)**2
>>> sp.optimize.minimize(f, [2, -1], method="Nelder-Mead")
message: Optimization terminated successfully.
success: True
status: 0
fun: 1.11527915993744e-10
x: [ 1.000e+00 1.000e+00]
nit: 58
nfev: 111
final_simplex: (array([[ 1.000e+00, 1.000e+00],
[ 1.000e+00, 1.000e+00],
[ 1.000e+00, 1.000e+00]]), array([ 1.115e-10, 1.537e-10, 4.988e-10]))
2.7.4.13. 全局优化器¶
如果您的问题不承认唯一的局部最小值(除非函数是凸函数,否则很难测试),并且您没有先验信息来初始化靠近解的优化,则可能需要全局优化器。
蛮力法:网格搜索¶
scipy.optimize.brute() 在给定的参数网格上评估函数,并返回对应于最小值的参数。参数由传递给 numpy.mgrid 的范围指定。默认情况下,每个方向都会执行 20 步。
>>> def f(x): # The rosenbrock function
... return .5*(1 - x[0])**2 + (x[1] - x[0]**2)**2
>>> sp.optimize.brute(f, ((-1, 2), (-1, 2)))
array([1.0000..., 1.0000...])
2.7.5. 使用 SciPy 进行优化的实用指南¶
2.7.5.1. 选择方法¶
所有方法都作为 scipy.optimize.minimize() 的 method 参数公开。

- 不知道梯度:
一般来说,即使您必须数值逼近梯度,也更倾向于使用 BFGS 或 L-BFGS。如果问题有约束或边界,这些也是省略参数
method时的默认值。在条件良好的问题上,Powell 和 Nelder-Mead 都是无梯度方法,在高维空间中效果很好,但它们在病态条件问题上会失效。
- 知道梯度:
BFGS 或 L-BFGS。
BFGS 的计算开销大于 L-BFGS,L-BFGS 又大于共轭梯度。另一方面,BFGS 通常需要的函数评估次数少于 CG。因此,对于优化计算成本低的函数,共轭梯度方法优于 BFGS。
- 使用 Hessian 矩阵:
如果您可以计算 Hessian 矩阵,则更倾向于使用牛顿法(Newton-CG 或 TCG)。
- 如果您的测量结果存在噪声:
使用 Nelder-Mead 或 Powell。
2.7.5.2. 使您的优化器更快¶
选择正确的方法(见上文),如果可以,请分析计算梯度和 Hessian 矩阵。
尽可能使用 预处理。
明智地选择初始化点。例如,如果您正在运行许多类似的优化,则可以使用另一个的结果来热启动一个。
如果您不需要使用参数
tol来进行精确计算,可以放宽容差。
2.7.5.3. 计算梯度¶
计算梯度,甚至更多的 Hessian 矩阵,非常繁琐,但值得付出努力。使用 Sympy 进行符号计算可能会有帮助。
警告
优化不收敛的一个非常常见的原因是人为错误地计算了梯度。您可以使用 scipy.optimize.check_grad() 来检查您的梯度是否正确。它返回给定梯度与数值计算的梯度之间的差的范数。
>>> sp.optimize.check_grad(f, jacobian, [2, -1])
np.float64(2.384185791015625e-07)
另请参见 scipy.optimize.approx_fprime() 以查找错误。
2.7.5.4. 综合练习¶
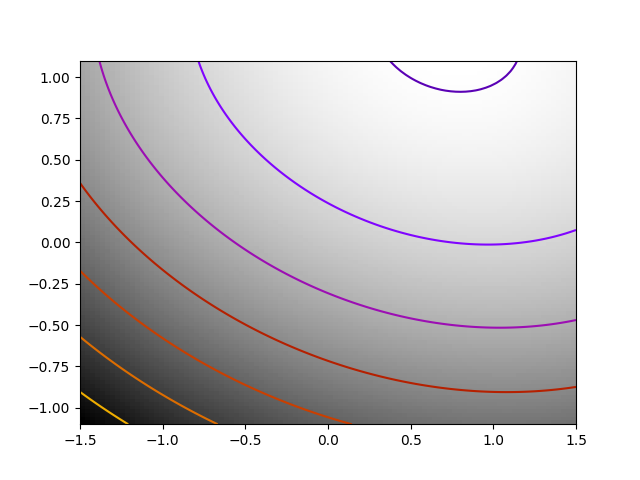
2.7.6. 特殊情况:非线性最小二乘¶
2.7.6.1. 最小化向量函数的范数¶
最小二乘问题(最小化向量函数的范数)具有特定的结构,可以在 Levenberg-Marquardt 算法(在 scipy.optimize.leastsq() 中实现)中使用。
让我们尝试最小化以下向量函数的范数。
>>> def f(x):
... return np.arctan(x) - np.arctan(np.linspace(0, 1, len(x)))
>>> x0 = np.zeros(10)
>>> sp.optimize.leastsq(f, x0)
(array([0. , 0.11111111, 0.22222222, 0.33333333, 0.44444444,
0.55555556, 0.66666667, 0.77777778, 0.88888889, 1. ]), 2)
这花费了 67 次函数评估(使用 'full_output=1' 检查)。如果我们自己计算范数并使用一个好的通用优化器(BFGS)会怎样?
>>> def g(x):
... return np.sum(f(x)**2)
>>> result = sp.optimize.minimize(g, x0, method="BFGS")
>>> result.fun
np.float64(2.6940...e-11)
BFGS 需要更多的函数调用,并且给出的结果精度较低。
注意
仅当输出向量的维度很大,并且大于要优化的参数数量时,leastsq 与 BFGS 相比才比较有趣。
警告
如果函数是线性的,则这是一个线性代数问题,应该使用 scipy.linalg.lstsq() 来解决。
2.7.6.2. 曲线拟合¶
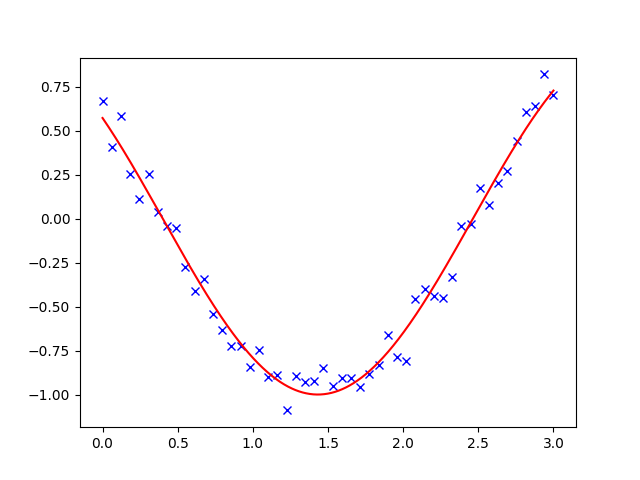
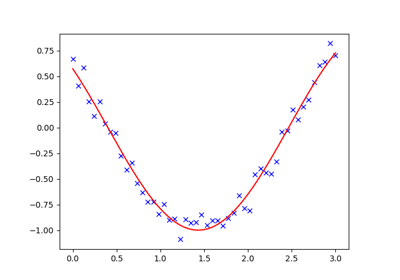
当将非线性函数拟合到数据时,经常会遇到最小二乘问题。虽然可以自己构建优化问题,但 SciPy 提供了一个辅助函数来实现此目的:scipy.optimize.curve_fit()
>>> def f(t, omega, phi):
... return np.cos(omega * t + phi)
>>> x = np.linspace(0, 3, 50)
>>> rng = np.random.default_rng(27446968)
>>> y = f(x, 1.5, 1) + .1*rng.normal(size=50)
>>> sp.optimize.curve_fit(f, x, y)
(array([1.4812..., 0.9999...]), array([[ 0.0003..., -0.0004...],
[-0.0004..., 0.0010...]]))
2.7.7. 带约束的优化¶
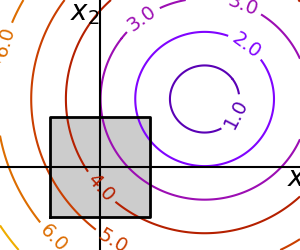
2.7.7.1. 边界约束¶
边界约束对应于限制优化的每个单独参数。请注意,一些最初未编写为边界约束的问题可以通过变量变换重写为边界约束。 scipy.optimize.minimize_scalar() 和 scipy.optimize.minimize() 都支持使用参数 bounds 的边界约束。
>>> def f(x):
... return np.sqrt((x[0] - 3)**2 + (x[1] - 2)**2)
>>> sp.optimize.minimize(f, np.array([0, 0]), bounds=((-1.5, 1.5), (-1.5, 1.5)))
message: CONVERGENCE: NORM_OF_PROJECTED_GRADIENT_<=_PGTOL
success: True
status: 0
fun: 1.5811388300841898
x: [ 1.500e+00 1.500e+00]
nit: 2
jac: [-9.487e-01 -3.162e-01]
nfev: 9
njev: 3
hess_inv: <2x2 LbfgsInvHessProduct with dtype=float64>
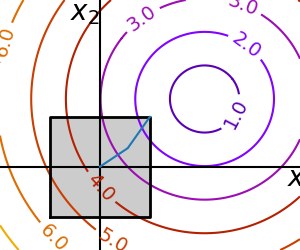
2.7.7.2. 一般约束¶
用函数指定等式和不等式约束: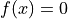 和
和 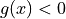 。
。
scipy.optimize.fmin_slsqp()序列最小二乘规划:等式和不等式约束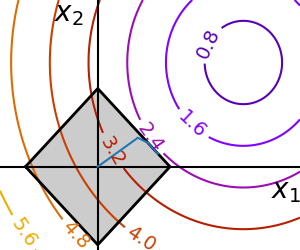
>>> def f(x): ... return np.sqrt((x[0] - 3)**2 + (x[1] - 2)**2) >>> def constraint(x): ... return np.atleast_1d(1.5 - np.sum(np.abs(x))) >>> x0 = np.array([0, 0]) >>> sp.optimize.minimize(f, x0, constraints={"fun": constraint, "type": "ineq"}) message: Optimization terminated successfully success: True status: 0 fun: 2.47487373504... x: [ 1.250e+00 2.500e-01] nit: 5 jac: [-7.071e-01 -7.071e-01] nfev: 15 njev: 5
警告
上述问题在统计学中被称为 Lasso 问题,并且存在非常高效的求解器(例如在 scikit-learn 中)。一般来说,当存在特定的求解器时,不要使用通用求解器。