3.2. Sympy：Python中的符号数学¶

作者：Fabian Pedregosa

什么是SymPy？SymPy是一个用于符号数学的Python库。它旨在成为Mathematica或Maple等系统的替代方案，同时尽可能地保持代码简单且易于扩展。SymPy完全用Python编写，不需要任何外部库。

SymPy文档和安装包可以在https://www.sympy.cn/找到。

3.2.1. SymPy入门 ¶

3.2.1.1. 将SymPy用作计算器 ¶

SymPy定义了三种数值类型：Real、Rational和Integer。

Rational类将有理数表示为两个Integers的配对：分子和分母，因此Rational(1, 2)表示1/2，Rational(5, 2)表示5/2，依此类推。

>>> importsympyassym
>>> a=sym.Rational(1,2)
>>> a
1/2
>>> a*2
1

SymPy在后台使用mpmath，这使得它能够使用任意精度算术进行计算。这样，一些特殊的常数，例如 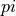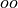$e$ 、 $pi$ 、 $oo$ （无穷大），被视为符号，并且可以以任意精度计算。

>>> sym.pi**2
pi**2
>>> sym.pi.evalf()
3.14159265358979
>>> (sym.pi+sym.exp(1)).evalf()
5.85987448204884

如您所见，evalf将表达式计算为浮点数。

还有一个表示数学无穷大的类，称为oo。

>>> sym.oo>99999
True
>>> sym.oo+1
oo

3.2.1.2. 符号 ¶

与其他计算机代数系统不同，在SymPy中，您必须显式声明符号变量。

>>> x=sym.Symbol('x')
>>> y=sym.Symbol('y')

然后您可以操作它们。

>>> x+y+x-y
2*x
>>> (x+y)**2
(x + y)**2

符号现在可以使用一些Python运算符进行操作：+、-、*、**（算术）、&、|、~、>>、<<（布尔）。

3.2.2. 代数运算 ¶

SymPy能够执行强大的代数运算。我们将了解一些最常用的运算：展开和化简。

3.2.2.1. 展开 ¶

使用此功能展开代数表达式。它将尝试取消嵌套幂和乘法。

>>> sym.expand((x+y)**3)
 3      2          2    3
x  + 3*x *y + 3*x*y  + y
>>> 3*x*y**2+3*y*x**2+x**3+y**3
 3      2          2    3
x  + 3*x *y + 3*x*y  + y

可以以关键字的形式提供更多选项。

>>> sym.expand(x+y,complex=True)
re(x) + re(y) + I*im(x) + I*im(y)
>>> sym.I*sym.im(x)+sym.I*sym.im(y)+sym.re(x)+sym.re(y)
re(x) + re(y) + I*im(x) + I*im(y)
>>> sym.expand(sym.cos(x+y),trig=True)
-sin(x)*sin(y) + cos(x)*cos(y)
>>> sym.cos(x)*sym.cos(y)-sym.sin(x)*sym.sin(y)
-sin(x)*sin(y) + cos(x)*cos(y)

3.2.2.2. 化简 ¶

如果您希望将表达式转换为更简单的形式，请使用simplify。

>>> sym.simplify((x+x*y)/x)
y + 1

化简是一个有点模糊的术语，并且存在比simplify更精确的替代方案：powsimp（指数化简）、trigsimp（用于三角表达式）、logcombine、radsimp，等等。

3.2.3. 微积分 ¶

3.2.3.1. 极限 ¶

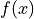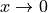在SymPy中，极限很容易使用，它们遵循语法limit(function, variable, point)，因此要计算 $f(x)$ 当 $x \rightarrow 0$ 时的极限，您可以发出limit(f, x, 0)。

>>> sym.limit(sym.sin(x)/x,x,0)
1

您还可以计算无穷大处的极限。

>>> sym.limit(x,x,sym.oo)
oo
>>> sym.limit(1/x,x,sym.oo)
0
>>> sym.limit(x**x,x,0)
1

3.2.3.2. 微分 ¶

您可以使用diff(func, var)对任何SymPy表达式进行微分。示例：

>>> sym.diff(sym.sin(x),x)
cos(x)
>>> sym.diff(sym.sin(2*x),x)
2*cos(2*x)
>>> sym.diff(sym.tan(x),x)
   2
tan (x) + 1

您可以通过以下方式检查它是否正确：

>>> sym.limit((sym.tan(x+y)-sym.tan(x))/y,y,0)
   1
-------
   2
cos (x)

这与以下等价，因为：

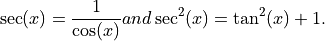
$\sec(x) = \frac{1}{\cos(x)} and \sec^2(x) = \tan^2(x) + 1.$

您也可以检查这一点。

>>> sym.trigsimp(sym.diff(sym.tan(x),x))
   1
-------
   2
cos (x)

可以使用diff(func, var, n)方法计算高阶导数。

>>> sym.diff(sym.sin(2*x),x,1)
2*cos(2*x)
>>> sym.diff(sym.sin(2*x),x,2)
-4*sin(2*x)
>>> sym.diff(sym.sin(2*x),x,3)
-8*cos(2*x)

3.2.3.3. 级数展开 ¶

SymPy还知道如何在某一点计算表达式的泰勒级数。使用series(expr, var)。

>>> sym.series(sym.cos(x),x)
     2    4
    x    x     / 6\
1 - -- + -- + O\x /
    2    24
>>> sym.series(1/sym.cos(x),x)
     2      4
    x    5*x     / 6\
1 + -- + ---- + O\x /
    2     24

3.2.3.4. 积分 ¶

SymPy支持通过integrate()工具对超越基本函数和特殊函数进行不定积分和定积分，该工具使用强大的扩展Risch-Norman算法以及一些启发式方法和模式匹配。您可以对基本函数进行积分。

>>> sym.integrate(6*x**5,x)
 6
x
>>> sym.integrate(sym.sin(x),x)
-cos(x)
>>> sym.integrate(sym.log(x),x)
x*log(x) - x
>>> sym.integrate(2*x+sym.sinh(x),x)
 2
x  + cosh(x)

特殊函数也很容易处理。

>>> sym.integrate(sym.exp(-x**2)*sym.erf(x),x)
  ____    2
\/ pi *erf (x)
--------------
      4

可以计算定积分。

>>> sym.integrate(x**3,(x,-1,1))
0
>>> sym.integrate(sym.sin(x),(x,0,sym.pi/2))
1
>>> sym.integrate(sym.cos(x),(x,-sym.pi/2,sym.pi/2))
2

也支持瑕积分。

>>> sym.integrate(sym.exp(-x),(x,0,sym.oo))
1
>>> sym.integrate(sym.exp(-x**2),(x,-sym.oo,sym.oo))
  ____
\/ pi

3.2.4. 方程求解 ¶

SymPy能够使用solveset()求解一元和多元代数方程。

>>> sym.solveset(x**4-1,x)
{-1, 1, -I, I}

如您所见，它以应该等于0的表达式作为第一个参数。它还对超越方程提供（有限的）支持。

>>> sym.solveset(sym.exp(x)+1,x)
{I*(2*n*pi + pi) | n in Integers}

对于多项式方程，另一种选择是factor。factor返回分解成不可约因式的多项式，并且能够计算不同域上的因式分解。

>>> f=x**4-3*x**2+1
>>> sym.factor(f)
/ 2        \ / 2        \
\x  - x - 1/*\x  + x - 1/
>>> sym.factor(f,modulus=5)
       2        2
(x - 2) *(x + 2)

SymPy还能够求解布尔方程，也就是说，确定某个布尔表达式是否可满足。为此，我们使用函数satisfiable。

>>> sym.satisfiable(x&y)
{x: True, y: True}

这告诉我们，当x和y都为True时，(x & y)为True。如果表达式不可能为真，即其参数的任何值都不能使表达式为真，它将返回False。

>>> sym.satisfiable(x&~x)
False

3.2.5. 线性代数 ¶

3.2.5.1. 矩阵 ¶

矩阵作为Matrix类的实例创建。

>>> sym.Matrix([[1,0],[0,1]])
[1  0]
[    ]
[0  1]

与NumPy数组不同，您也可以在其中放入符号。

>>> x,y=sym.symbols('x, y')
>>> A=sym.Matrix([[1,x],[y,1]])
>>> A
[1  x]
[    ]
[y  1]
>>> A**2
[x*y + 1    2*x  ]
[                ]
[  2*y    x*y + 1]

3.2.5.2. 微分方程 ¶

SymPy能够求解（一些）常微分方程。要求解微分方程，请使用dsolve。首先，通过将cls=Function传递给symbols函数来创建一个未定义的函数。

>>> f,g=sym.symbols('f g',cls=sym.Function)

f和g现在是未定义的函数。我们可以调用f(x)，它将表示一个未知函数。

>>> f(x)
f(x)
>>> f(x).diff(x,x)+f(x)
         2
        d
f(x) + ---(f(x))
         2
       dx
>>> sym.dsolve(f(x).diff(x,x)+f(x),f(x))
f(x) = C1*sin(x) + C2*cos(x)

可以向此函数提供关键字参数，以便在找到最佳可能的解析系统时提供帮助。例如，如果您知道这是一个可分离方程，则可以使用关键字hint='separable'强制dsolve将其解析为可分离方程。

>>> sym.dsolve(sym.sin(x)*sym.cos(f(x))+sym.cos(x)*sym.sin(f(x))*f(x).diff(x),f(x),hint='separable')
               /  C1  \                    /  C1  \
 [f(x) = - acos|------| + 2*pi, f(x) = acos|------|]
               \cos(x)/                    \cos(x)/