2.7.4.5. 在平坦邻域中寻找最小值

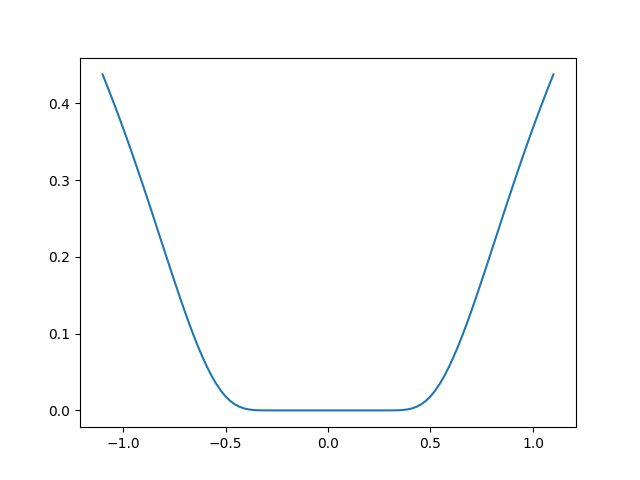
寻找最小值的练习。这个练习很难，因为函数在最小值附近非常平坦（所有导数都为零）。因此，梯度信息不可靠。

该函数在 [0, 0] 处存在最小值。挑战是从 x0 = [1, 1] 开始，将最小值收敛到 1e-7 内。

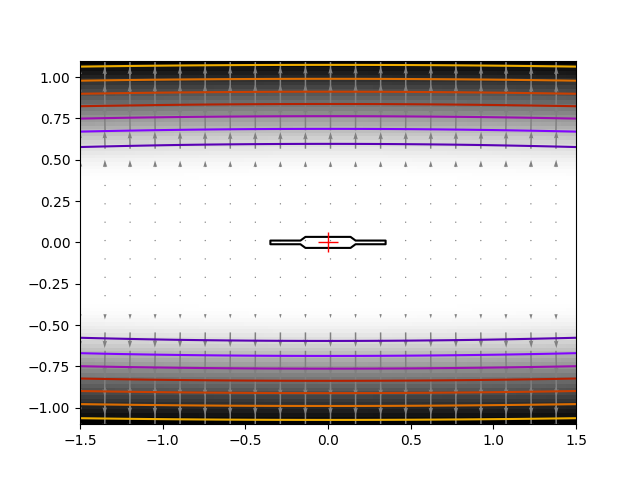
我们在这里采用的解决方案是放弃使用梯度或基于局部差异的信息，并依赖于 Powell 算法。经过 162 次函数评估，我们得到了 1e-8 的解。

import numpy as np
import scipy as sp
import matplotlib.pyplot as plt


def f(x):
    return np.exp(-1 / (0.01 * x[0] ** 2 + x[1] ** 2))


# A well-conditionned version of f:
def g(x):
    return f([10 * x[0], x[1]])


# The gradient of g. We won't use it here for the optimization.
def g_prime(x):
    r = np.sqrt(x[0] ** 2 + x[1] ** 2)
    return 2 / r**3 * g(x) * x / r


result = sp.optimize.minimize(g, [1, 1], method="Powell", tol=1e-10)
x_min = result.x

一些漂亮的绘图

plt.figure(0)
plt.clf()
t = np.linspace(-1.1, 1.1, 100)
plt.plot(t, f([0, t]))

plt.figure(1)
plt.clf()
X, Y = np.mgrid[-1.5:1.5:100j, -1.1:1.1:100j]  # type: ignore[misc]
plt.imshow(f([X, Y]).T, cmap="gray_r", extent=(-1.5, 1.5, -1.1, 1.1), origin="lower")
plt.contour(X, Y, f([X, Y]), cmap="gnuplot")

# Plot the gradient
dX, dY = g_prime([0.1 * X[::5, ::5], Y[::5, ::5]])
# Adjust for our preconditioning
dX *= 0.1
plt.quiver(X[::5, ::5], Y[::5, ::5], dX, dY, color=".5")

# Plot our solution
plt.plot(x_min[0], x_min[1], "r+", markersize=15)

plt.show()

• 
•