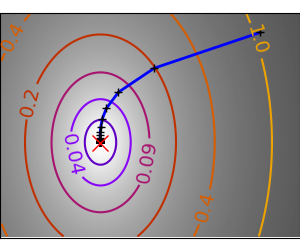
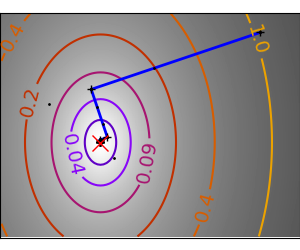
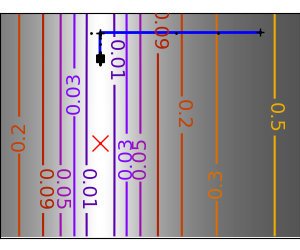
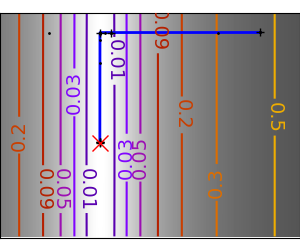
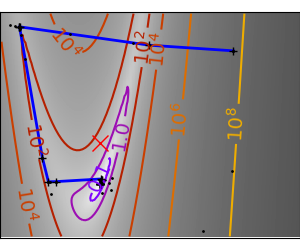
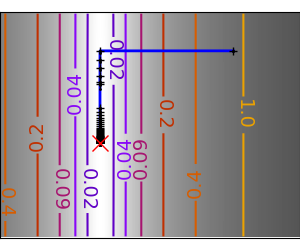
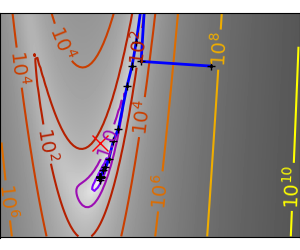
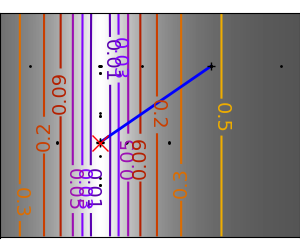
2.7.4.11. 梯度下降

一个演示梯度下降的示例，通过创建跟踪优化器演变过程的图形。

import numpy as np
import matplotlib.pyplot as plt
import scipy as sp

import collections
import sys
import os

sys.path.append(os.path.abspath("helper"))
from cost_functions import (
    mk_quad,
    mk_gauss,
    rosenbrock,
    rosenbrock_prime,
    rosenbrock_hessian,
    LoggingFunction,
    CountingFunction,
)

x_min, x_max = -1, 2
y_min, y_max = 2.25 / 3 * x_min - 0.2, 2.25 / 3 * x_max - 0.2

一个用于在等高线上打印值的格式化程序

def super_fmt(value):
    if value > 1:
        if np.abs(int(value) - value) < 0.1:
            out = f"$10^{{{int(value):d}}}$"
        else:
            out = f"$10^{{{value:.1f}}}$"
    else:
        value = np.exp(value - 0.01)
        if value > 0.1:
            out = f"{value:1.1f}"
        elif value > 0.01:
            out = f"{value:.2f}"
        else:
            out = f"{value:.2e}"
    return out

梯度下降算法不使用：它只是一个玩具，使用 scipy 的 optimize.fmin_cg

def gradient_descent(x0, f, f_prime, hessian=None, adaptative=False):
    x_i, y_i = x0
    all_x_i = []
    all_y_i = []
    all_f_i = []

    for i in range(1, 100):
        all_x_i.append(x_i)
        all_y_i.append(y_i)
        all_f_i.append(f([x_i, y_i]))
        dx_i, dy_i = f_prime(np.asarray([x_i, y_i]))
        if adaptative:
            # Compute a step size using a line_search to satisfy the Wolf
            # conditions
            step = sp.optimize.line_search(
                f,
                f_prime,
                np.r_[x_i, y_i],
                -np.r_[dx_i, dy_i],
                np.r_[dx_i, dy_i],
                c2=0.05,
            )
            step = step[0]
            if step is None:
                step = 0
        else:
            step = 1
        x_i += -step * dx_i
        y_i += -step * dy_i
        if np.abs(all_f_i[-1]) < 1e-16:
            break
    return all_x_i, all_y_i, all_f_i


def gradient_descent_adaptative(x0, f, f_prime, hessian=None):
    return gradient_descent(x0, f, f_prime, adaptative=True)


def conjugate_gradient(x0, f, f_prime, hessian=None):
    all_x_i = [x0[0]]
    all_y_i = [x0[1]]
    all_f_i = [f(x0)]

    def store(X):
        x, y = X
        all_x_i.append(x)
        all_y_i.append(y)
        all_f_i.append(f(X))

    sp.optimize.minimize(
        f, x0, jac=f_prime, method="CG", callback=store, options={"gtol": 1e-12}
    )
    return all_x_i, all_y_i, all_f_i


def newton_cg(x0, f, f_prime, hessian):
    all_x_i = [x0[0]]
    all_y_i = [x0[1]]
    all_f_i = [f(x0)]

    def store(X):
        x, y = X
        all_x_i.append(x)
        all_y_i.append(y)
        all_f_i.append(f(X))

    sp.optimize.minimize(
        f,
        x0,
        method="Newton-CG",
        jac=f_prime,
        hess=hessian,
        callback=store,
        options={"xtol": 1e-12},
    )
    return all_x_i, all_y_i, all_f_i


def bfgs(x0, f, f_prime, hessian=None):
    all_x_i = [x0[0]]
    all_y_i = [x0[1]]
    all_f_i = [f(x0)]

    def store(X):
        x, y = X
        all_x_i.append(x)
        all_y_i.append(y)
        all_f_i.append(f(X))

    sp.optimize.minimize(
        f, x0, method="BFGS", jac=f_prime, callback=store, options={"gtol": 1e-12}
    )
    return all_x_i, all_y_i, all_f_i


def powell(x0, f, f_prime, hessian=None):
    all_x_i = [x0[0]]
    all_y_i = [x0[1]]
    all_f_i = [f(x0)]

    def store(X):
        x, y = X
        all_x_i.append(x)
        all_y_i.append(y)
        all_f_i.append(f(X))

    sp.optimize.minimize(
        f, x0, method="Powell", callback=store, options={"ftol": 1e-12}
    )
    return all_x_i, all_y_i, all_f_i


def nelder_mead(x0, f, f_prime, hessian=None):
    all_x_i = [x0[0]]
    all_y_i = [x0[1]]
    all_f_i = [f(x0)]

    def store(X):
        x, y = X
        all_x_i.append(x)
        all_y_i.append(y)
        all_f_i.append(f(X))

    sp.optimize.minimize(
        f, x0, method="Nelder-Mead", callback=store, options={"ftol": 1e-12}
    )
    return all_x_i, all_y_i, all_f_i

在这些问题上运行不同的优化器

levels = {}

for index, ((f, f_prime, hessian), optimizer) in enumerate(
    (
        (mk_quad(0.7), gradient_descent),
        (mk_quad(0.7), gradient_descent_adaptative),
        (mk_quad(0.02), gradient_descent),
        (mk_quad(0.02), gradient_descent_adaptative),
        (mk_gauss(0.02), gradient_descent_adaptative),
        (
            (rosenbrock, rosenbrock_prime, rosenbrock_hessian),
            gradient_descent_adaptative,
        ),
        (mk_gauss(0.02), conjugate_gradient),
        ((rosenbrock, rosenbrock_prime, rosenbrock_hessian), conjugate_gradient),
        (mk_quad(0.02), newton_cg),
        (mk_gauss(0.02), newton_cg),
        ((rosenbrock, rosenbrock_prime, rosenbrock_hessian), newton_cg),
        (mk_quad(0.02), bfgs),
        (mk_gauss(0.02), bfgs),
        ((rosenbrock, rosenbrock_prime, rosenbrock_hessian), bfgs),
        (mk_quad(0.02), powell),
        (mk_gauss(0.02), powell),
        ((rosenbrock, rosenbrock_prime, rosenbrock_hessian), powell),
        (mk_gauss(0.02), nelder_mead),
        ((rosenbrock, rosenbrock_prime, rosenbrock_hessian), nelder_mead),
    )
):
    # Compute a gradient-descent
    x_i, y_i = 1.6, 1.1
    counting_f_prime = CountingFunction(f_prime)
    counting_hessian = CountingFunction(hessian)
    logging_f = LoggingFunction(f, counter=counting_f_prime.counter)
    all_x_i, all_y_i, all_f_i = optimizer(
        np.array([x_i, y_i]), logging_f, counting_f_prime, hessian=counting_hessian
    )

    # Plot the contour plot
    if not max(all_y_i) < y_max:
        x_min *= 1.2
        x_max *= 1.2
        y_min *= 1.2
        y_max *= 1.2
    x, y = np.mgrid[x_min:x_max:100j, y_min:y_max:100j]
    x = x.T
    y = y.T

    plt.figure(index, figsize=(3, 2.5))
    plt.clf()
    plt.axes([0, 0, 1, 1])

    X = np.concatenate((x[np.newaxis, ...], y[np.newaxis, ...]), axis=0)
    z = np.apply_along_axis(f, 0, X)
    log_z = np.log(z + 0.01)
    plt.imshow(
        log_z,
        extent=[x_min, x_max, y_min, y_max],
        cmap=plt.cm.gray_r,
        origin="lower",
        vmax=log_z.min() + 1.5 * np.ptp(log_z),
    )
    contours = plt.contour(
        log_z,
        levels=levels.get(f),
        extent=[x_min, x_max, y_min, y_max],
        cmap=plt.cm.gnuplot,
        origin="lower",
    )
    levels[f] = contours.levels
    plt.clabel(contours, inline=1, fmt=super_fmt, fontsize=14)

    plt.plot(all_x_i, all_y_i, "b-", linewidth=2)
    plt.plot(all_x_i, all_y_i, "k+")

    plt.plot(logging_f.all_x_i, logging_f.all_y_i, "k.", markersize=2)

    plt.plot([0], [0], "rx", markersize=12)

    plt.xticks(())
    plt.yticks(())
    plt.xlim(x_min, x_max)
    plt.ylim(y_min, y_max)
    plt.draw()

    plt.figure(index + 100, figsize=(4, 3))
    plt.clf()
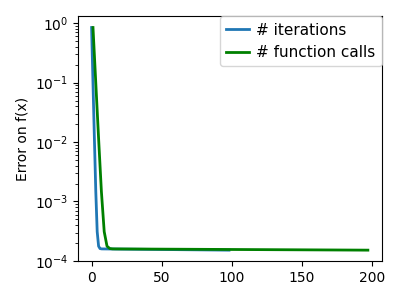
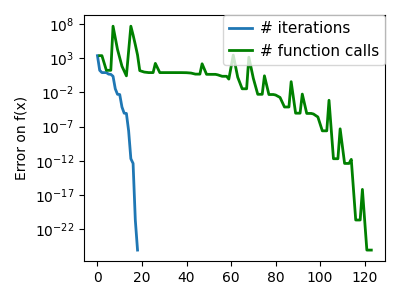
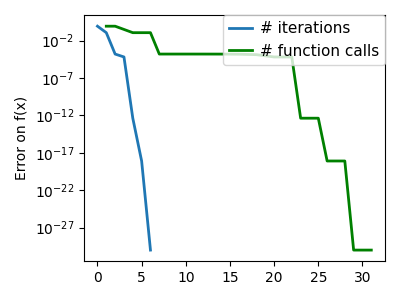
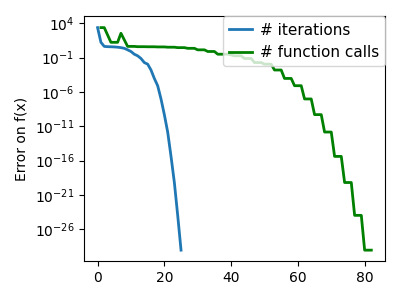
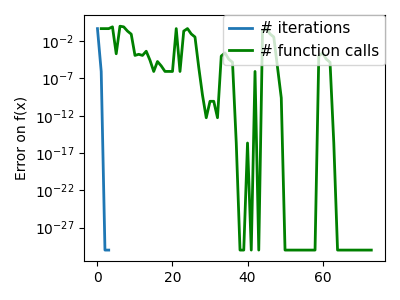
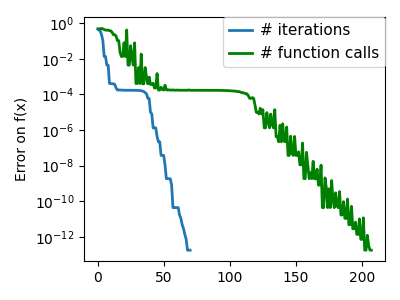
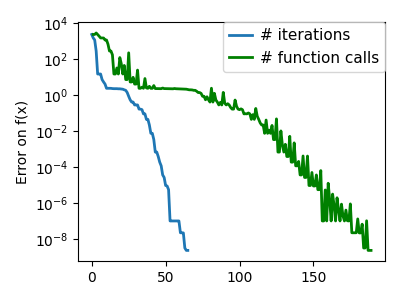
    plt.semilogy(np.maximum(np.abs(all_f_i), 1e-30), linewidth=2, label="# iterations")
    plt.ylabel("Error on f(x)")
    plt.semilogy(
        logging_f.counts,
        np.maximum(np.abs(logging_f.all_f_i), 1e-30),
        linewidth=2,
        color="g",
        label="# function calls",
    )
    plt.legend(
        loc="upper right",
        frameon=True,
        prop={"size": 11},
        borderaxespad=0,
        handlelength=1.5,
        handletextpad=0.5,
    )
    plt.tight_layout()
    plt.draw()

• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 

/opt/hostedtoolcache/Python/3.12.6/x64/lib/python3.12/site-packages/scipy/optimize/_linesearch.py:312: LineSearchWarning: The line search algorithm did not converge
  alpha_star, phi_star, old_fval, derphi_star = scalar_search_wolfe2(
/home/runner/work/scientific-python-lectures/scientific-python-lectures/advanced/mathematical_optimization/examples/plot_gradient_descent.py:70: LineSearchWarning: The line search algorithm did not converge
  step = sp.optimize.line_search(
/home/runner/work/scientific-python-lectures/scientific-python-lectures/advanced/mathematical_optimization/examples/plot_gradient_descent.py:234: RuntimeWarning: More than 20 figures have been opened. Figures created through the pyplot interface (`matplotlib.pyplot.figure`) are retained until explicitly closed and may consume too much memory. (To control this warning, see the rcParam `figure.max_open_warning`). Consider using `matplotlib.pyplot.close()`.
  plt.figure(index, figsize=(3, 2.5))
/home/runner/work/scientific-python-lectures/scientific-python-lectures/advanced/mathematical_optimization/examples/plot_gradient_descent.py:179: OptimizeWarning: Unknown solver options: ftol
  sp.optimize.minimize(