1.5.11.2. 非线性最小二乘曲线拟合：在地形激光雷达数据中应用于点提取

本练习的目的是将模型拟合到某些数据。本教程中使用的数据是激光雷达数据，并在以下介绍性段落中进行了详细描述。如果您很着急并且现在想练习，请跳过它并直接转到 加载和可视化。

引言

激光雷达系统是光学测距仪，它分析散射光的特性来测量距离。它们中的大多数都向目标发射短光脉冲并记录反射信号。然后处理此信号以提取激光雷达系统与目标之间的距离。

地形激光雷达系统是嵌入在机载平台中的此类系统。它们测量平台与地球之间的距离，以便提供有关地球地形的信息（有关更多详细信息，请参见 [1]）。

在本教程中，目标是分析激光雷达系统记录的波形 [2]。此类信号包含峰值，其中心和幅度允许计算命中目标的位置和某些特征。当激光束的足迹在地球表面周围为 1 米时，该光束可以在双向传播过程中命中多个目标（例如地面和树木或建筑物的顶部）。然后，激光束击中的每个目标的贡献之和会产生一个具有多个峰值的复杂信号，每个峰值都包含有关一个目标的信息。

一种从这些数据中提取信息的最先进方法是将其分解为高斯函数的总和，其中每个函数表示激光束击中的目标的贡献。

因此，我们使用 scipy.optimize 模块将波形拟合到一个或多个高斯函数的总和。

加载和可视化

使用以下命令加载第一个波形：

>>> import numpy as np

>>> waveform_1 = np.load('intro/scipy/summary-exercises/examples/waveform_1.npy')

并将其可视化：

>>> import matplotlib.pyplot as plt

>>> t = np.arange(len(waveform_1))

>>> plt.plot(t, waveform_1) 

[<matplotlib.lines.Line2D object at ...>]

>>> plt.show()

如下所示，此波形是长度为 80 个 bin 的信号，在第 15 纳秒 bin 中具有一个峰值，其幅度约为 30。此外，噪声基准水平约为 3。这些值可用于初始解。

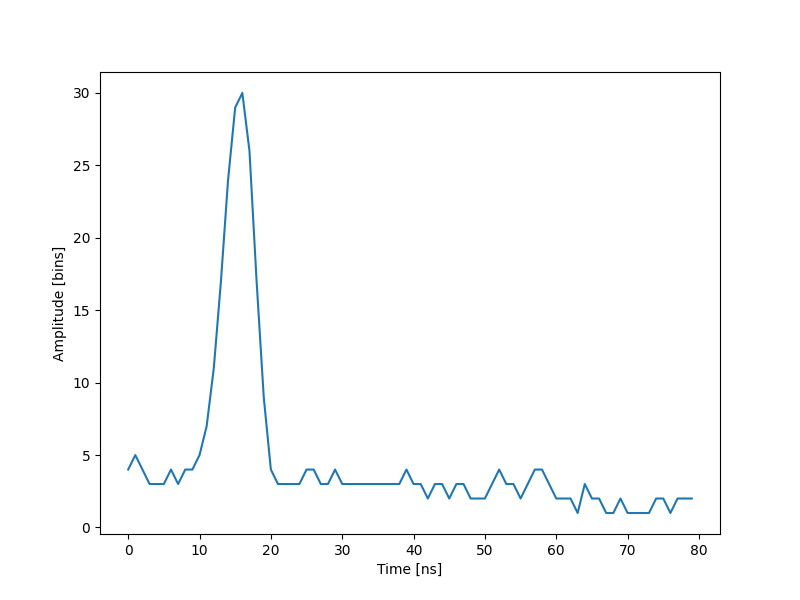
../../../_images/sphx_glr_plot_optimize_lidar_data_001.png

使用简单高斯模型拟合波形

该信号非常简单，可以建模为单个高斯函数和对应于背景噪声的偏移量。要使用该函数拟合信号，我们必须

  • 定义模型

  • 提出初始解

  • 调用 scipy.optimize.leastsq

模型

由以下公式定义的高斯函数：

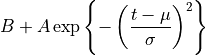
B + A \exp\left\{-\left(\frac{t-\mu}{\sigma}\right)^2\right\}

可以用 python 定义为：

>>> def model(t, coeffs):

...    return coeffs[0] + coeffs[1] * np.exp( - ((t-coeffs[2])/coeffs[3])**2 )

其中

  • coeffs[0] 是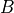 B（噪声）

  • coeffs[1] 是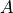 A（幅度）

  • coeffs[2] 是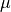 \mu（中心）

  • coeffs[3] 是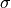 \sigma（宽度）

初始解

通过检查确定的一个可能的初始解是：

>>> x0 = np.array([3, 30, 15, 1], dtype=float)

拟合

scipy.optimize.leastsq 最小化作为参数给出的函数的平方和。基本上，要最小化的函数是残差（数据和模型之间的差异）

>>> def residuals(coeffs, y, t):

...     return y - model(t, coeffs)

因此，让我们通过使用以下参数调用 scipy.optimize.leastsq() 来获得我们的解：

  • 要最小化的函数

  • 初始解

  • 要传递给函数的其他参数

>>> import scipy as sp

>>> t = np.arange(len(waveform_1))

>>> x, flag = sp.optimize.leastsq(residuals, x0, args=(waveform_1, t))

>>> x

array([ 2.70363, 27.82020, 15.47924,  3.05636])

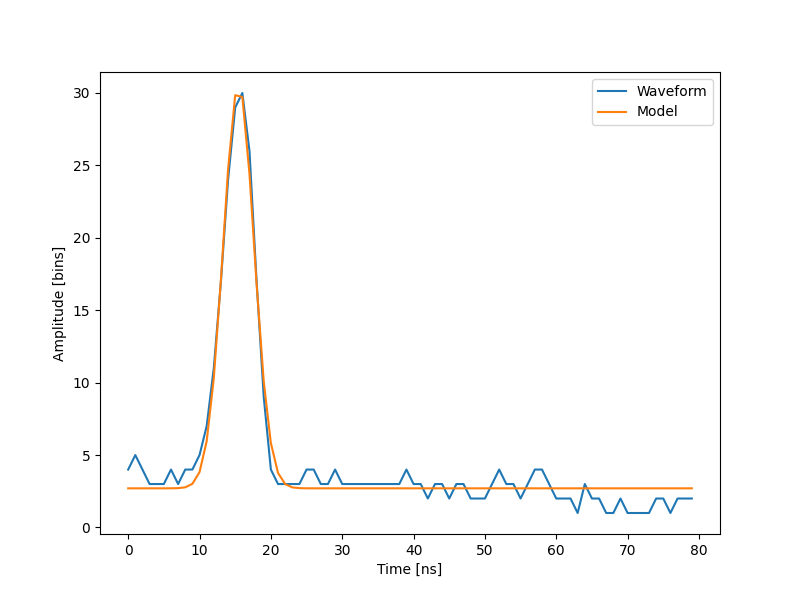
并可视化解

fig, ax = plt.subplots(figsize=(8, 6))

plt.plot(t, waveform_1, t, model(t, x))

plt.xlabel("Time [ns]")

plt.ylabel("Amplitude [bins]")

plt.legend(["Waveform", "Model"])

plt.show()
../../../_images/sphx_glr_plot_optimize_lidar_data_fit_001.png

备注：从 scipy v0.8 及更高版本开始，您应该改用 scipy.optimize.curve_fit()，它将模型和数据作为参数，因此您不再需要定义残差。

更进一步

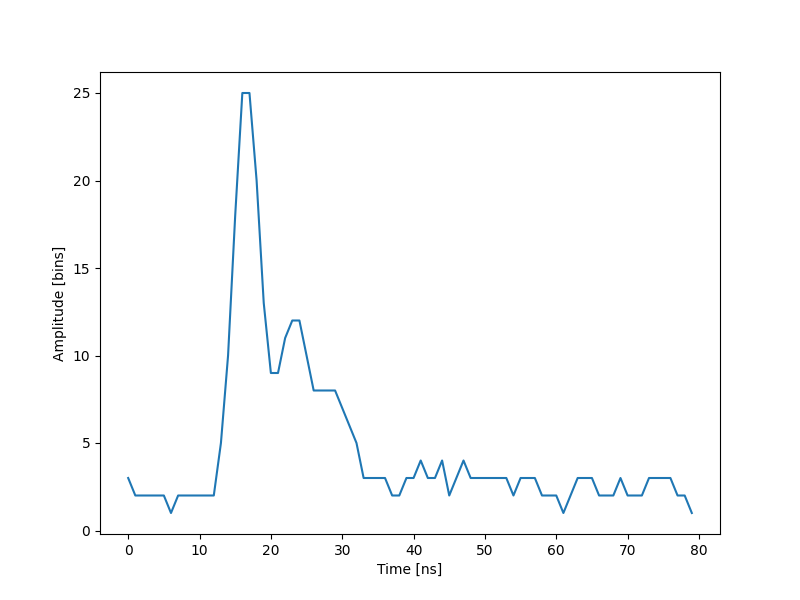
  • 尝试使用更复杂的波形（例如 waveform_2.npy），其中包含三个显着的峰值。您必须调整模型，该模型现在是高斯函数的总和，而不是只有一个高斯峰。

../../../_images/sphx_glr_plot_optimize_lidar_complex_data_001.png

  • 在某些情况下，编写一个显式函数来计算雅可比矩阵比让 leastsq 以数值方式估计它更快。创建一个函数来计算残差的雅可比矩阵，并将其用作 leastsq 的输入。

  • 当我们想要检测信号中非常小的峰值，或者当初始猜测与良好解相差太远时，算法给出的结果通常并不令人满意。为模型的参数添加约束可以克服此类限制。我们可以添加的先验知识的一个示例是我们变量的符号（它们都是正数）。

  • 请参阅 解决方案。

  • 进一步练习：比较 scipy.optimize.leastsq() 的结果以及在添加边界约束时可以使用 scipy.optimize.fmin_slsqp() 获得的结果。