1.5.11.1. Sprogø 站的最大风速预测

本练习的目标是预测每 50 年发生一次的最大风速，即使没有该时间段的测量数据。可用的数据仅来自位于丹麦的 Sprogø 气象站的 21 年测量数据。首先，将给出统计步骤，然后用 scipy.interpolate 模块中的函数进行说明。最后，鼓励感兴趣的读者从原始数据计算结果，并采用略微不同的方法。

统计方法

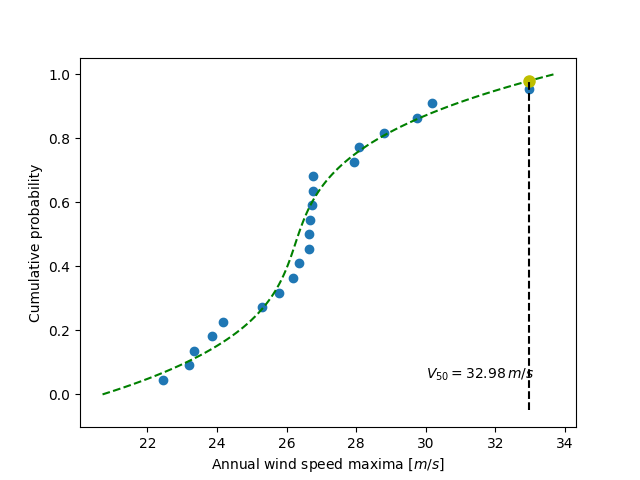
假设年最大值符合正态概率密度函数。但是，不会估计这种函数，因为它给出了风速最大值的概率。要找到每 50 年发生一次的最大风速，需要采用相反的方法，需要从定义的概率中找到结果。这就是分位数函数的作用，本练习的目标是找到它。在当前模型中，假设每 50 年发生一次的最大风速被定义为上 2% 的分位数。

根据定义，分位数函数是累积分布函数的逆函数。后者描述了年最大值的概率分布。在本练习中，给定年份 i 的累积概率 p_i 被定义为 p_i = i/(N+1)，其中 N = 21 是测量的年份数。因此，可以计算每个测量的风速最大值的累积概率。从这些实验点，scipy.interpolate 模块对于拟合分位数函数将非常有用。最后，将从 2% 分位数的累积概率评估 50 年最大值。

计算累积概率

年风速最大值已经计算出来并保存在 NumPy 格式的 examples/max-speeds.npy 文件中，因此将使用 NumPy 加载它们。

>>> import numpy as np

>>> max_speeds = np.load('intro/scipy/summary-exercises/examples/max-speeds.npy')

>>> years_nb = max_speeds.shape[0]

遵循上一节中累积概率定义 p_i，对应的值将是

>>> cprob = (np.arange(years_nb, dtype=np.float32) + 1)/(years_nb + 1)

并且假设它们符合给定的风速。

>>> sorted_max_speeds = np.sort(max_speeds)

使用 UnivariateSpline 进行预测

在本节中，将使用 UnivariateSpline 类估计分位数函数，该类可以从点表示样条曲线。默认行为是构建 3 次样条曲线，并且点可以根据其可靠性具有不同的权重。变体是 InterpolatedUnivariateSpline 和 LSQUnivariateSpline，它们的错误检查将发生变化。如果需要 2D 样条曲线，则提供 BivariateSpline 类族。所有这些用于 1D 和 2D 样条曲线的类都使用 FITPACK Fortran 子例程，这就是为什么可以通过 splrep 和 splev 函数（分别用于表示和评估样条曲线）获得更低级别的库访问。此外，还提供不使用 FITPACK 参数的插值函数，以方便使用。

对于 Sprogø 最大风速，将使用 UnivariateSpline，因为 3 次样条曲线似乎可以正确拟合数据。

>>> import scipy as sp

>>> quantile_func = sp.interpolate.UnivariateSpline(cprob, sorted_max_speeds)

现在将从完整概率范围内评估分位数函数。

>>> nprob = np.linspace(0, 1, 100)

>>> fitted_max_speeds = quantile_func(nprob)

在当前模型中，每 50 年发生一次的最大风速被定义为上 2% 的分位数。因此，累积概率值为

>>> fifty_prob = 1. - 0.02

因此，可以估计每 50 年发生的暴风风速为

>>> fifty_wind = quantile_func(fifty_prob)

>>> fifty_wind

array(32.97989825...)

现在将结果收集到 Matplotlib 图像中。

../../../_images/sphx_glr_plot_cumulative_wind_speed_prediction_001.png

解决方案: Python 源 文件

使用 Gumbel 分布进行练习

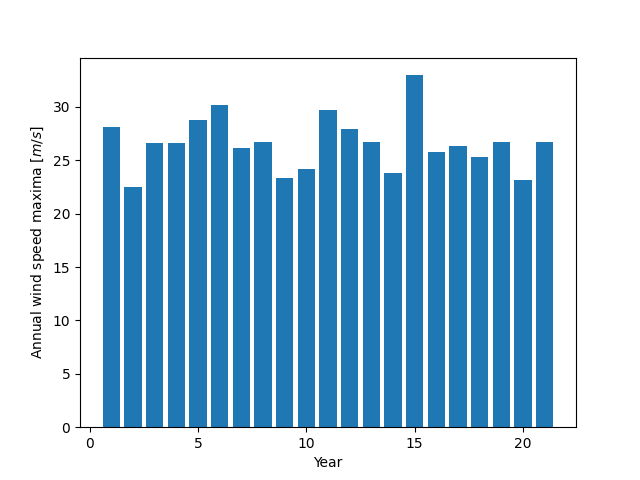
现在邀请感兴趣的读者使用 21 年测量的风速进行练习。测量周期约为 90 分钟（原始周期约为 10 分钟，但文件大小已减少，以简化练习设置）。数据存储在 NumPy 格式的 examples/sprog-windspeeds.npy 文件中。在完成练习之前，请不要查看绘图的源代码。

  • 第一步是使用 NumPy 找到年最大值，并将其绘制成 matplotlib 条形图。

../../../_images/sphx_glr_plot_sprog_annual_maxima_001.png

解决方案: Python 源 文件

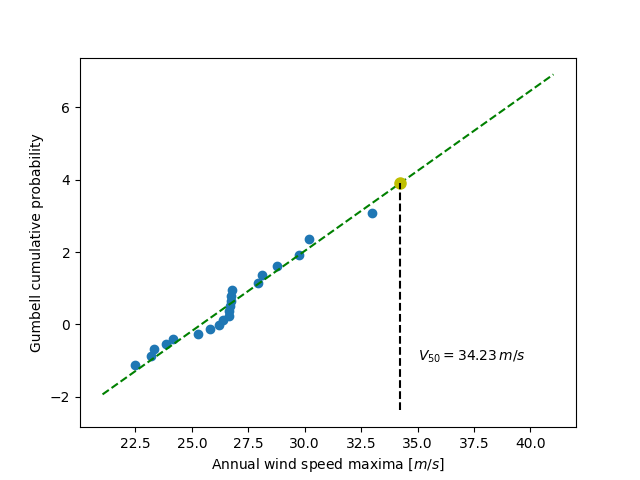
  • 第二步是将 Gumbel 分布应用于定义为 -log( -log(p_i) ) 的累积概率 p_i，以拟合线性分位数函数（请记住，您可以定义 UnivariateSpline 的次数）。将年最大值与 Gumbel 分布绘制在一起应该会得到以下图像。

../../../_images/sphx_glr_plot_gumbell_wind_speed_prediction_001.png

解决方案: Python 源 文件

  • 最后一步是找到每 50 年发生一次的最大风速为 34.23 m/s。