1.3.5. 一些练习

1.3.5.1. 数组操作

1. 构建二维数组（无需显式输入）

   [[1,  6, 11],
    [2,  7, 12],
    [3,  8, 13],
    [4,  9, 14],
    [5, 10, 15]]
   

   并生成一个包含其第二行和第四行的数组。

2. 将数组的每一列

   >>> import numpy as np
   >>> a = np.arange(25).reshape(5, 5)
   

   按元素除以数组 b = np.array([1., 5, 10, 15, 20])。（提示：np.newaxis）。

3. 较难的：生成一个 10 x 3 的随机数数组（范围为 [0,1]）。对于每一行，选择最接近 0.5 的数字。

   • 使用 abs 和 argmin 找到每行的最接近的列 j。

   • 使用花式索引提取数字。（提示：a[i,j] – 数组 i 必须包含对应于 j 中内容的行号。）

1.3.5.2. 图片操作：给脸部加相框

让我们从浣熊的图像开始，对 NumPy 数组进行一些操作。 scipy 使用 scipy.datasets.face 函数提供了此图像的二维数组

>>> import scipy as sp
>>> face = sp.datasets.face(gray=True)  # 2D grayscale image

以下是一些我们可以通过操作获得的图像：使用不同的颜色映射，裁剪图像，改变图像的某些部分。

• 让我们使用 matplotlib 的 imshow 函数显示图像。

  >>> import matplotlib.pyplot as plt
  >>> face = sp.datasets.face(gray=True)
  >>> plt.imshow(face)
  <matplotlib.image.AxesImage object at 0x...>
  

• 人脸以伪彩色显示。必须指定颜色映射才能以灰色显示。

  创建一个图像的数组，中心更窄，例如，

  >>> plt.imshow(face, cmap=plt.cm.gray)
  <matplotlib.image.AxesImage object at 0x...>
  

• 从图像的所有边界移除 100 像素。要检查结果，使用 imshow 显示这个新数组。

  现在，我们将用黑色挂坠给脸部加相框。为此，我们

  >>> crop_face = face[100:-100, 100:-100]
  

• 需要创建一个对应于我们要设置为黑色的像素的掩码。人脸的中心大约在 (660, 330) 处，因此我们通过以下条件定义了掩码：(y-300)**2 + (x-660)**2

  然后，我们将值 0 分配给对应于掩码的图像像素。语法非常简单直观

  >>> sy, sx = face.shape
  >>> y, x = np.ogrid[0:sy, 0:sx] # x and y indices of pixels
  >>> y.shape, x.shape
  ((768, 1), (1, 1024))
  >>> centerx, centery = (660, 300) # center of the image
  >>> mask = ((y - centery)**2 + (x - centerx)**2) > 230**2 # circle
  

  后续：将此练习的所有说明复制到名为

  >>> face[mask] = 0
  >>> plt.imshow(face)
  <matplotlib.image.AxesImage object at 0x...>
  

• face_locket.py 的脚本中，然后在 IPython 中使用 %run face_locket.py 执行此脚本。

  将圆形更改为椭圆形。

  1.3.5.3. 数据统计

populations.txt 中的数据描述了加拿大北部 20 年间野兔和猞猁（以及胡萝卜）的数量

根据 populations.txt 中的数据，计算并打印…

>>> data = np.loadtxt('data/populations.txt')
>>> year, hares, lynxes, carrots = data.T  # trick: columns to variables

>>> import matplotlib.pyplot as plt
>>> plt.axes([0.2, 0.1, 0.5, 0.8])
<Axes: >
>>> plt.plot(year, hares, year, lynxes, year, carrots)
[<matplotlib.lines.Line2D object at ...>, ...]
>>> plt.legend(('Hare', 'Lynx', 'Carrot'), loc=(1.05, 0.5))
<matplotlib.legend.Legend object at ...>

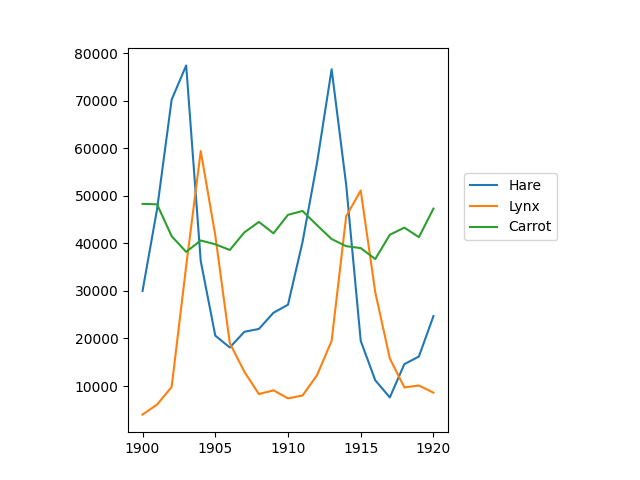
每个物种在该时期的年份中的平均数量和标准差。

1. 每个物种数量最多的年份。

2. 每年数量最多的物种。（提示：argsort 和 np.array(['H', 'L', 'C']) 的花式索引）

3. 任何一个物种的数量超过 50000 的年份。（提示：比较和 np.any）

4. 每个物种数量最少的 2 个年份。（提示：argsort，花式索引）

5. 比较（绘制）野兔数量变化（见 help(np.gradient)）和猞猁数量。检查相关性（见 help(np.corrcoef)）。

6. … 所有这些都不用 for 循环。

解决方案： Python 源 文件

1.3.5.4. 粗略积分近似

编写一个函数 f(a, b, c)，它返回 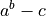。在参数范围 [0,1] x [0,1] x [0,1] 内，构建一个 24x12x6 数组，其中包含其值。

用平均值近似该体积上的三维积分

在该体积上的三维积分

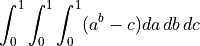
精确结果为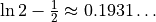： – 您的相对误差是多少？

（提示：使用按元素操作和广播。您可以使用 np.ogrid 在给定范围内生成一定数量的点，例如使用 np.ogrid[0:1:20j]。）

提醒 Python 函数

def f(a, b, c):
    return some_result

解决方案： Python 源 文件

1.3.5.5. 曼德博集合

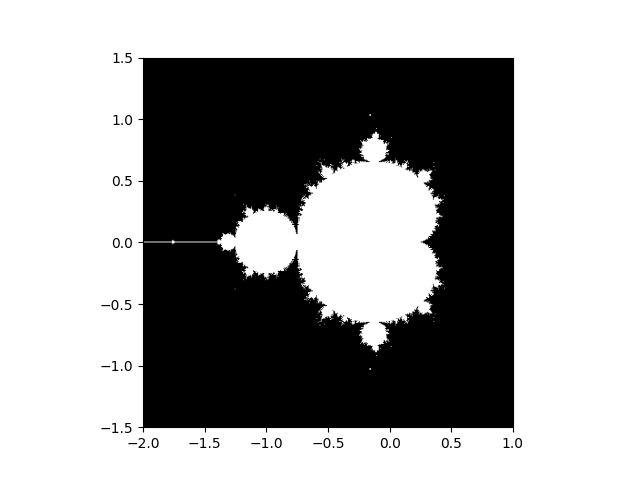
编写一个脚本，用于计算曼德博分形。曼德博迭代

N_max = 50
some_threshold = 50

c = x + 1j*y

z = 0
for j in range(N_max):
    z = z**2 + c

如果 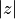< some_threshold，则点 (x, y) 属于曼德博集合。

通过以下方式进行计算

1. 在范围 [-2, 1] x [-1.5, 1.5] 内构造 c = x + 1j*y 值的网格

2. 执行迭代

3. 形成二维布尔掩码，指示哪些点在集合中

4. 使用以下方式将结果保存到图像中

>>> import matplotlib.pyplot as plt
>>> plt.imshow(mask.T, extent=[-2, 1, -1.5, 1.5])
<matplotlib.image.AxesImage object at ...>
>>> plt.gray()
>>> plt.savefig('mandelbrot.png')

解决方案： Python 源 文件

1.3.5.6. 马尔可夫链

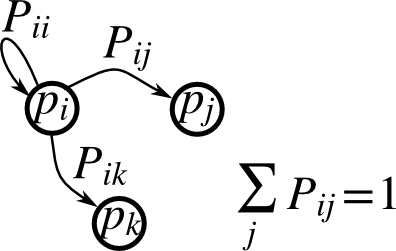
马尔可夫链转移矩阵 P 和状态上的概率分布 p

1. 0 <= P[i,j] <= 1：从状态 i 转移到状态 j 的概率

2. 转移规则：

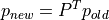
3. all(sum(P, axis=1) == 1)，p.sum() == 1：归一化

编写一个使用 5 个状态的脚本，并

• 构建一个随机矩阵，并对每一行进行归一化，使其成为一个转移矩阵。

• 从一个随机的（归一化的）概率分布 p 开始，并进行 50 步 => p_50

• 计算稳态分布：P.T 的特征向量，其特征值为 1（数值上：最接近 1） => p_stationary

请记住对特征向量进行归一化 — 我没有…

• 检查 p_50 和 p_stationary 是否等于容差 1e-5

工具箱：np.random，@，np.linalg.eig，约简，abs()，argmin，比较，all，np.linalg.norm 等。

解决方案： Python 源 文件