2.5.1. 引言¶
(稠密)矩阵是
数学对象
用于存储二维数值数组的数据结构
重要特征
- 为所有元素一次性分配内存
通常是一块连续的内存块,例如 NumPy ndarray
快速访问单个元素 (*)
2.5.1.1. 为什么使用稀疏矩阵?¶
对于稠密矩阵,内存增长速度与 n**2 成正比
一个小例子(双精度矩阵)
>>> import numpy as np >>> import matplotlib.pyplot as plt >>> x = np.linspace(0, 1e6, 10) >>> plt.plot(x, 8.0 * (x**2) / 1e6, lw=5) [<matplotlib.lines.Line2D object at ...>] >>> plt.xlabel('size n') Text(...'size n') >>> plt.ylabel('memory [MB]') Text(...'memory [MB]')
2.5.1.2. 稀疏矩阵与稀疏矩阵存储方案¶
稀疏矩阵是指几乎为空的矩阵
存储所有零元素是浪费的 -> 只存储非零元素
可以理解为压缩
优点:节省大量内存
缺点:访问单个元素速度较慢,但取决于实际的存储方案。
2.5.1.3. 典型应用¶
- 偏微分方程 (PDE) 的求解
有限元方法
机械工程、电气工程、物理学等
- 图论
在 (i, j) 处存在非零元素表示节点 i 与节点 j 相连
- 自然语言处理
在 (i, j) 处存在非零元素表示文档 i 包含单词 j
…
2.5.1.4. 先决条件¶
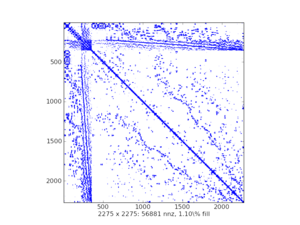
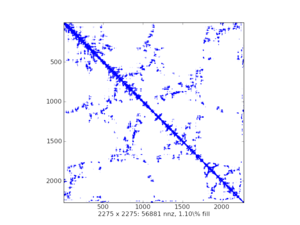
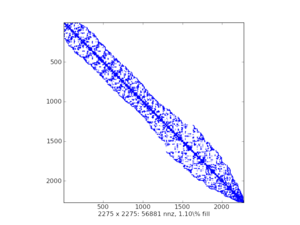
2.5.1.5. 稀疏结构可视化¶
spy()来自matplotlib示例图表