2.5.3. 线性系统求解器¶
稀疏矩阵/特征值问题求解器位于
scipy.sparse.linalg- 子模块
dsolve: 用于求解线性系统的直接分解方法isolve: 用于求解线性系统的迭代方法eigen: 稀疏特征值问题求解器
所有求解器都可以从以下位置访问
>>> import scipy as sp >>> sp.sparse.linalg.__all__ ['ArpackError', 'ArpackNoConvergence', ..., 'use_solver']
2.5.3.1. 稀疏直接求解器¶
- 默认求解器:SuperLU
包含在 SciPy 中
实数和复数系统
单精度和双精度
- 可选:umfpack
实数和复数系统
仅双精度
建议用于性能
包装器现在位于
scikits.umfpack查看 Nathaniel Smith 的新
scikits.suitesparse
示例¶
导入整个模块,并查看其文档字符串
>>> help(sp.sparse.linalg.spsolve) Help on function spsolve in module scipy.sparse.linalg._dsolve.linsolve: ...
superlu 和 umfpack 都可以使用(如果安装了后者),如下所示
准备一个线性系统
>>> import numpy as np >>> mtx = sp.sparse.spdiags([[1, 2, 3, 4, 5], [6, 5, 8, 9, 10]], [0, 1], 5, 5, "csc") >>> mtx.toarray() array([[ 1, 5, 0, 0, 0], [ 0, 2, 8, 0, 0], [ 0, 0, 3, 9, 0], [ 0, 0, 0, 4, 10], [ 0, 0, 0, 0, 5]]) >>> rhs = np.array([1, 2, 3, 4, 5], dtype=np.float32)
以单精度实数形式求解
>>> mtx1 = mtx.astype(np.float32) >>> x = sp.sparse.linalg.spsolve(mtx1, rhs, use_umfpack=False) >>> print(x) [106. -21. 5.5 -1.5 1. ] >>> print("Error: %s" % (mtx1 * x - rhs)) Error: [0. 0. 0. 0. 0.]
以双精度实数形式求解
>>> mtx2 = mtx.astype(np.float64) >>> x = sp.sparse.linalg.spsolve(mtx2, rhs, use_umfpack=True) >>> print(x) [106. -21. 5.5 -1.5 1. ] >>> print("Error: %s" % (mtx2 * x - rhs)) Error: [0. 0. 0. 0. 0.]
以单精度复数形式求解
>>> mtx1 = mtx.astype(np.complex64) >>> x = sp.sparse.linalg.spsolve(mtx1, rhs, use_umfpack=False) >>> print(x) [106. +0.j -21. +0.j 5.5+0.j -1.5+0.j 1. +0.j] >>> print("Error: %s" % (mtx1 * x - rhs)) Error: [0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j]
以双精度复数形式求解
>>> mtx2 = mtx.astype(np.complex128) >>> x = sp.sparse.linalg.spsolve(mtx2, rhs, use_umfpack=True) >>> print(x) [106. +0.j -21. +0.j 5.5+0.j -1.5+0.j 1. +0.j] >>> print("Error: %s" % (mtx2 * x - rhs)) Error: [0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j]
"""
Solve a linear system
=======================
Construct a 1000x1000 lil_array and add some values to it, convert it
to CSR format and solve A x = b for x:and solve a linear system with a
direct solver.
"""
import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
rng = np.random.default_rng(27446968)
mtx = sp.sparse.lil_array((1000, 1000), dtype=np.float64)
mtx[0, :100] = rng.random(100)
mtx[1, 100:200] = mtx[[0], :100]
mtx.setdiag(rng.random(1000))
plt.clf()
plt.spy(mtx, marker=".", markersize=2)
plt.show()
mtx = mtx.tocsr()
rhs = rng.random(1000)
x = sp.sparse.linalg.spsolve(mtx, rhs)
print(f"residual: {np.linalg.norm(mtx @ x - rhs)!r}")
2.5.3.2. 迭代求解器¶
isolve模块包含以下求解器bicg(双共轭梯度)bicgstab(双共轭梯度稳定化)cg(共轭梯度) - 仅对称正定矩阵cgs(共轭梯度平方)gmres(广义最小残差)minres(最小残差)qmr(准最小残差)
常用参数¶
必需
- A{稀疏数组/矩阵,密集数组/矩阵,线性算子}
线性系统的 N×N 矩阵。
- b{数组,矩阵}
线性系统的右侧。形状为 (N,) 或 (N,1)。
可选
- x0{数组,矩阵}
解的初始猜测。
- tol浮点数
在终止之前要达到的相对容差。
- maxiter整数
最大迭代次数。即使未达到指定的容差,迭代也将停止在 maxiter 步后。
- M{稀疏数组/矩阵,密集数组/矩阵,线性算子}
A 的预处理器。预处理器应该近似 A 的逆。有效的预处理显着提高了收敛速度,这意味着需要更少的迭代次数才能达到给定的误差容差。
- callback函数
在每次迭代后调用的用户提供的函数。它以 callback(xk) 的形式调用,其中 xk 是当前的解向量。
线性算子类¶
执行矩阵向量积的通用接口
有用的抽象,它允许在求解器中使用密集矩阵和稀疏矩阵,以及 *无矩阵* 解
具有 *形状* 和 *matvec()*(以及一些可选参数)
示例
>>> import numpy as np
>>> import scipy as sp
>>> def mv(v):
... return np.array([2 * v[0], 3 * v[1]])
...
>>> A = sp.sparse.linalg.LinearOperator((2, 2), matvec=mv)
>>> A
<2x2 _CustomLinearOperator with dtype=float64>
>>> A.matvec(np.ones(2))
array([2., 3.])
>>> A * np.ones(2)
array([2., 3.])
关于预处理的一些说明¶
特定于问题
通常很难开发
- 如果不知道,请尝试 ILU
在
scipy.sparse.linalg中可用,如spilu()
2.5.3.3. 特征值问题求解器¶
eigen 模块¶
arpack* 一组 Fortran77 子例程,旨在解决大规模特征值问题lobpcg(局部最优块预处理共轭梯度方法) * 与 PyAMG 结合使用效果很好 * 由 Nathan Bell 提供的示例""" Compute eigenvectors and eigenvalues using a preconditioned eigensolver ======================================================================= In this example Smoothed Aggregation (SA) is used to precondition the LOBPCG eigensolver on a two-dimensional Poisson problem with Dirichlet boundary conditions. """ import numpy as np import scipy as sp import matplotlib.pyplot as plt from pyamg import smoothed_aggregation_solver from pyamg.gallery import poisson N = 100 K = 9 A = poisson((N, N), format="csr") # create the AMG hierarchy ml = smoothed_aggregation_solver(A) # initial approximation to the K eigenvectors X = np.random.random((A.shape[0], K)) # preconditioner based on ml M = ml.aspreconditioner() # compute eigenvalues and eigenvectors with LOBPCG W, V = sp.sparse.linalg.lobpcg(A, X, M=M, tol=1e-8, largest=False) # plot the eigenvectors plt.figure(figsize=(9, 9)) for i in range(K): plt.subplot(3, 3, i + 1) plt.title("Eigenvector %d" % i) plt.pcolor(V[:, i].reshape(N, N)) plt.axis("equal") plt.axis("off") plt.show()
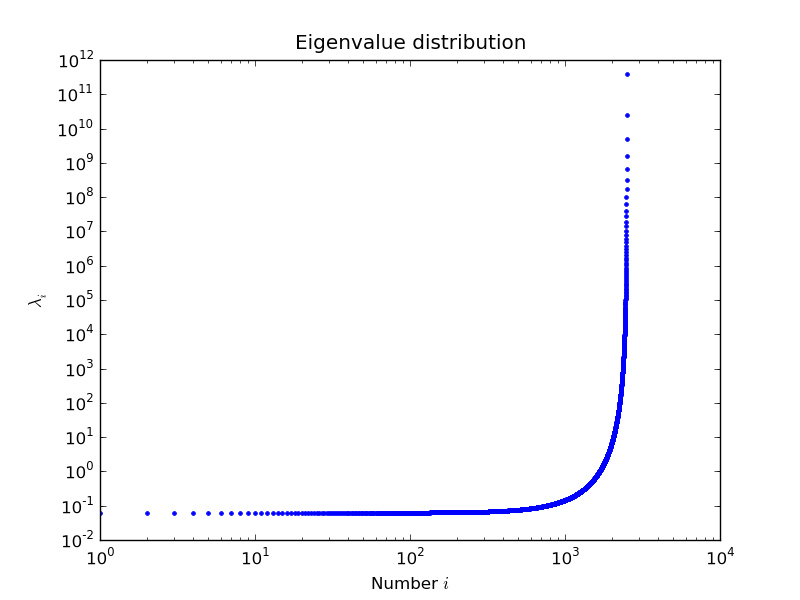
由 Nils Wagner 提供的示例
输出
$ python examples/lobpcg_sakurai.py Results by LOBPCG for n=2500 [ 0.06250083 0.06250028 0.06250007] Exact eigenvalues [ 0.06250005 0.0625002 0.06250044] Elapsed time 7.01