2.4. 代码优化¶
作者: Gaël Varoquaux
本章讨论使 Python 代码运行更快的策略。
2.4.1. 优化工作流程¶
使其工作：以简单易读的方式编写代码。
使其可靠地工作：编写自动化测试用例，确保你的算法是正确的，并且如果破坏了它，测试将捕获破坏。
通过对简单用例进行性能分析来优化代码，找到瓶颈并加速这些瓶颈，找到更好的算法或实现。请记住，应该在现实示例上的性能分析与代码的简单性和执行速度之间找到权衡。为了高效工作，最好使用持续时间约为 10 秒的性能分析运行。
2.4.2. Python 代码性能分析¶
2.4.2.1. Timeit¶
在 IPython 中，使用 timeit (https://docs.pythonlang.cn/3/library/timeit.html) 来计时基本操作
In [1]: import numpy as np
In [2]: a = np.arange(1000)
In [3]: %timeit a ** 2
902 ns +- 1.03 ns per loop (mean +- std. dev. of 7 runs, 1,000,000 loops each)
In [4]: %timeit a ** 2.1
15.7 us +- 22.3 ns per loop (mean +- std. dev. of 7 runs, 100,000 loops each)
In [5]: %timeit a * a
1.01 us +- 1.96 ns per loop (mean +- std. dev. of 7 runs, 1,000,000 loops each)
使用它来指导你在不同策略之间进行选择。
注意
对于长时间运行的调用，使用 %time 而不是 %timeit；它不太精确但速度更快
2.4.2.2. 性能分析器¶
当你有一个大型程序需要进行性能分析时很有用，例如 以下文件
# For this example to run, you also need the 'ica.py' file
import numpy as np
import scipy as sp
from ica import fastica
# @profile # uncomment this line to run with line_profiler
def test():
rng = np.random.default_rng()
data = rng.random((5000, 100))
u, s, v = sp.linalg.svd(data)
pca = u[:, :10].T @ data
results = fastica(pca.T, whiten=False)
if __name__ == "__main__":
test()
注意
这结合了两种无监督学习技术：主成分分析 (PCA) 和独立成分分析 (ICA)。PCA 是一种降维技术，即一种使用更少维度来解释数据中观察到的方差的算法。ICA 是一种源分离技术，例如用于混合通过多个传感器记录的多个信号。如果传感器数量多于信号数量，则首先进行 PCA，然后进行 ICA 可能很有用。有关更多信息，请参阅：scikits-learn 中的 FastICA 示例。
要运行它，你还需要下载 ica 模块。在 IPython 中，我们可以计时脚本
In [6]: %run -t demo.py
IPython CPU timings (estimated):
User : 14.3929 s.
System: 0.256016 s.
并对其进行性能分析
In [7]: %run -p demo.py
916 function calls in 14.551 CPU seconds
Ordered by: internal time
ncalls tottime percall cumtime percall filename:lineno (function)
1 14.457 14.457 14.479 14.479 decomp.py:849 (svd)
1 0.054 0.054 0.054 0.054 {method 'random_sample' of 'mtrand.RandomState' objects}
1 0.017 0.017 0.021 0.021 function_base.py:645 (asarray_chkfinite)
54 0.011 0.000 0.011 0.000 {numpy.core._dotblas.dot}
2 0.005 0.002 0.005 0.002 {method 'any' of 'numpy.ndarray' objects}
6 0.001 0.000 0.001 0.000 ica.py:195 (gprime)
6 0.001 0.000 0.001 0.000 ica.py:192 (g)
14 0.001 0.000 0.001 0.000 {numpy.linalg.lapack_lite.dsyevd}
19 0.001 0.000 0.001 0.000 twodim_base.py:204 (diag)
1 0.001 0.001 0.008 0.008 ica.py:69 (_ica_par)
1 0.001 0.001 14.551 14.551 {execfile}
107 0.000 0.000 0.001 0.000 defmatrix.py:239 (__array_finalize__)
7 0.000 0.000 0.004 0.001 ica.py:58 (_sym_decorrelation)
7 0.000 0.000 0.002 0.000 linalg.py:841 (eigh)
172 0.000 0.000 0.000 0.000 {isinstance}
1 0.000 0.000 14.551 14.551 demo.py:1 (<module>)
29 0.000 0.000 0.000 0.000 numeric.py:180 (asarray)
35 0.000 0.000 0.000 0.000 defmatrix.py:193 (__new__)
35 0.000 0.000 0.001 0.000 defmatrix.py:43 (asmatrix)
21 0.000 0.000 0.001 0.000 defmatrix.py:287 (__mul__)
41 0.000 0.000 0.000 0.000 {numpy.core.multiarray.zeros}
28 0.000 0.000 0.000 0.000 {method 'transpose' of 'numpy.ndarray' objects}
1 0.000 0.000 0.008 0.008 ica.py:97 (fastica)
...
显然，svd（在 decomp.py 中）是我们花费大部分时间的地方，也就是瓶颈。我们必须找到一种方法来加快此步骤的速度，或避免此步骤（算法优化）。在代码的其余部分上花费时间是没有意义的。
2.4.2.3. 行性能分析器¶
性能分析器告诉我们哪个函数花费了大部分时间，但没有告诉我们它在哪里被调用。
为此，我们使用 line_profiler：在源文件中，我们用 @profile 装饰一些我们想要检查的函数（无需导入它）
@profile
def test():
rng = np.random.default_rng()
data = rng.random((5000, 100))
u, s, v = linalg.svd(data)
pca = u[:, :10] @ data
results = fastica(pca.T, whiten=False)
然后我们使用 kernprof 命令运行脚本，并使用开关 -l, --line-by-line 和 -v, --view 来使用逐行性能分析器并在保存结果之外查看结果
$ kernprof -l -v demo.py
Wrote profile results to demo.py.lprof
Timer unit: 1e-06 s
Total time: 1.27874 s
File: demo.py
Function: test at line 9
Line # Hits Time Per Hit % Time Line Contents
==============================================================
9 @profile
10 def test():
11 1 69.0 69.0 0.0 rng = np.random.default_rng()
12 1 2453.0 2453.0 0.2 data = rng.random((5000, 100))
13 1 1274715.0 1274715.0 99.7 u, s, v = sp.linalg.svd(data)
14 1 413.0 413.0 0.0 pca = u[:, :10].T @ data
15 1 1094.0 1094.0 0.1 results = fastica(pca.T, whiten=False)
SVD 占用了所有时间。我们需要优化这一行。
2.4.3. 使代码运行更快¶
一旦我们确定了瓶颈，我们就需要使相应的代码运行得更快。
2.4.3.1. 算法优化¶
首先要寻找的是算法优化：是否有方法计算更少或更好？
对于问题的更高级别的视图，对算法背后的数学有很好的理解会有所帮助。但是，找到简单的更改并不少见，例如 **将计算或内存分配移到 for 循环之外**，这会带来很大的收益。
SVD 示例¶
在以上两个示例中，SVD - 奇异值分解 - 是最耗时的部分。实际上，此算法的计算成本大约为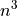 
，其中 n 为输入矩阵的大小。
但是，在这两个示例中，我们没有使用 SVD 的所有输出，而仅使用其第一个返回值的前几行。如果我们使用 SciPy 的 svd 实现，我们可以请求 SVD 的不完整版本。请注意，SciPy 中的线性代数实现比 NumPy 中的更丰富，应优先使用。
In [8]: %timeit np.linalg.svd(data)
1 loops, best of 3: 14.5 s per loop
In [9]: import scipy as sp
In [10]: %timeit sp.linalg.svd(data)
1 loops, best of 3: 14.2 s per loop
In [11]: %timeit sp.linalg.svd(data, full_matrices=False)
1 loops, best of 3: 295 ms per loop
In [12]: %timeit np.linalg.svd(data, full_matrices=False)
1 loops, best of 3: 293 ms per loop
然后我们可以利用此见解来 优化之前的代码
def test():
rng = np.random.default_rng()
data = rng.random((5000, 100))
u, s, v = sp.linalg.svd(data, full_matrices=False)
pca = u[:, :10].T @ data
results = fastica(pca.T, whiten=False)
In [13]: import demo
In [14]: %timeit demo.
demo.fastica demo.np demo.prof.pdf demo.py demo.pyc
demo.linalg demo.prof demo.prof.png demo.py.lprof demo.test
In [15]: %timeit demo.test()
ica.py:65: RuntimeWarning: invalid value encountered in sqrt
W = (u * np.diag(1.0/np.sqrt(s)) * u.T) * W # W = (W * W.T) ^{-1/2} * W
1 loops, best of 3: 17.5 s per loop
In [16]: import demo_opt
In [17]: %timeit demo_opt.test()
1 loops, best of 3: 208 ms per loop
真正的非完整 SVD，例如仅计算前 10 个特征向量，可以使用 arpack 计算，arpack 在 scipy.sparse.linalg.eigsh 中可用。
2.4.4. 编写更快的数值代码¶
关于 NumPy 高级用法的完整讨论可以在第 高级 NumPy 章或文章 The NumPy array: a structure for efficient numerical computation（van der Walt 等人）中找到。在这里，我们只讨论一些常见的技巧来使代码更快。
向量化 for 循环
找到使用 NumPy 数组避免 for 循环的技巧。为此，掩码和索引数组可能很有用。
广播
使用 广播 对尽可能小的数组进行操作，然后再将它们组合起来。
就地操作
In [18]: a = np.zeros(1e7) In [19]: %timeit global a ; a = 0*a 10 loops, best of 3: 111 ms per loop In [20]: %timeit global a ; a *= 0 10 loops, best of 3: 48.4 ms per loop
注意：我们需要在 timeit 中使用 global a 以使其工作，因为它正在赋值给 a，因此将其视为局部变量。
在内存方面要轻松：使用视图，而不是副本
复制大型数组与对它们进行简单的数值运算一样昂贵
In [21]: a = np.zeros(1e7) In [22]: %timeit a.copy() 10 loops, best of 3: 124 ms per loop In [23]: %timeit a + 1 10 loops, best of 3: 112 ms per loop
注意缓存效应
当内存访问分组时，它会更便宜：以连续方式访问大型数组比随机访问快得多。这意味着除其他事项外，**较小的步长更快**（参见 CPU 缓存效应）
In [24]: c = np.zeros((1e4, 1e4), order='C') In [25]: %timeit c.sum(axis=0) 1 loops, best of 3: 3.89 s per loop In [26]: %timeit c.sum(axis=1) 1 loops, best of 3: 188 ms per loop In [27]: c.strides Out[27]: (80000, 8)
这就是 Fortran 顺序或 C 顺序可能对操作产生很大影响的原因
In [28]: rng = np.random.default_rng() In [29]: a = rng.random((20, 2**18)) In [30]: b = rng.random((20, 2**18)) In [31]: %timeit b @ a.T 9.06 ms +- 25.2 us per loop (mean +- std. dev. of 7 runs, 100 loops each) In [32]: c = np.ascontiguousarray(a.T) In [33]: %timeit b @ c 9.92 ms +- 400 us per loop (mean +- std. dev. of 7 runs, 100 loops each)
请注意，复制数据以解决此效果可能不值得
In [34]: %timeit c = np.ascontiguousarray(a.T) 14.4 ms +- 46.1 us per loop (mean +- std. dev. of 7 runs, 100 loops each)
使用 numexpr 可以帮助自动优化代码以获得此类效果。
使用编译代码
一旦你确定所有高级优化都已探索，最后的办法是将热点（即大部分时间花费的几行或几个函数）转移到编译代码中。对于编译代码，首选选项是使用 Cython：它很容易将现有的 Python 代码转换为编译代码，并且通过良好地使用 NumPy 支持，可以对 NumPy 数组生成高效的代码，例如通过展开循环。
警告
对于上述所有内容：分析和计时你的选择。不要根据理论考虑来进行优化。
2.4.4.1. 其他链接¶
如果你需要分析内存使用情况，可以尝试 memory_profiler
如果你需要分析到 C 扩展，可以尝试使用 Python 中的 gperftools 和 yep。
如果您想跟踪代码随时间的性能，例如在您向存储库提交新代码时，可以尝试：asv
如果您需要一些交互式可视化，为什么不尝试一下RunSnakeRun